Inscription / Connexion Nouveau Sujet
Moment d'une force equilibre
Bonsoir,
Je vous demande de l'aide avec cet exercice là. C'est la première fois que j'essaye et je ne sais pas par où commencer.
On considère un gouvernail de bateau, et on simplifie l'objet sous la forme d'un cercle de rayon r et de centre O (en ce point la rotation se fait sans frottements). On applique au point P une force F--> de norme F.
Quel est le moment de la force par rapport à O (expression littérale), le moment de la
force par rapport à A ? On précisera bien le sens et la direction du vecteur obtenu
Le résultat dépend-il de l'angle ߙ?
Merci d'avance
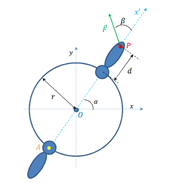
Je crois que pour trouver OP il faut faire: r + d cos alpha et r+d sin de alpha et pour trouver F cos (180 - (alpha+beta) et sinus de 180 - (alpha +beta )
Il s'agit bien du produit de l'intensité de la force par le bras de levier mais celui-ci s'obtient en considérant la projection orthogonale de O sur la droite passant par P dirigée par le vecteur force. Fais un schéma soigné pour t'aider.
bonjour vanoise,
je viens m'incruster sur le topic car je suis avec Doo sur l'exercice c'est moi qui lui ai conseiller de venir ici. On discute en meme temps sur whatsapp
donc pour le moment de F au point O on a
Mo()=F.OP.sin

o(
)= F^OP (desolé j'ai pas trouvé le symbole vectorielle) ce vecteur est
 au plan (xy) et dirigé vers le haut
au plan (xy) et dirigé vers le haut
jusque la ca me parait coherent et le resultat ne depend pas d'alpha
J'espere que c'est bon jusque la?
Par contre pour le point d'aplication en A, je ne comprend pas. Je presume qu'il s'agit d'une autre force, disons F2, dans le meme sens que F, mais comment je trouve l'angle entre x' et F2?
Du coup, j'ai fait ça:
Je ne sais pas si je dois le faire par rapport a x et si je dois développer un peu plus la réponse
D'accord avec les formules fournies par neo62950
Le bras de levier est la distance OH sur le schéma en supposant l'existence d'un angle droit en H.
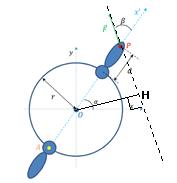
parfait c'est deja ca. Merci
Par contre je ne vois vraiment pas pour le point d'application en A. Un debut de piste?
J'ai répondu aux interrogations de doo sur la notion de bras de levier mais l'énoncé ne parle pas de moment de force par rapport à un axe mais bien de vecteur moment de force en un point. Les réponses attendues font donc intervenir un produit vectoriel comme proposé par neo62950 hier soir à 20h16.
bonjour, merci pour ces reponse.
Donc si je comprend bien j'ai juste a remplacer OP par AP dans le moment.
Soit MA(= F.AP.sin
 ?
?
Donc l'angle alpha n'entre toujours pas en jeu?
La force a appliqué en A pour ne pas que la roue tourne est une force d'intensite egale a F mais de sens et de direction contraire a F?
Les réponses attendues sont très probablement :
Pour que la roue ne tourne pas, la somme des moments en O des forces extérieures doit être nulle. Je choisis le calcul des moments en O car ainsi, le moment du poids de la barre, calculé au centre de gravité O, est le vecteur nul. La force de vecteur vérifie donc :



