Inscription / Connexion Nouveau Sujet
moment d'inertie
salut,
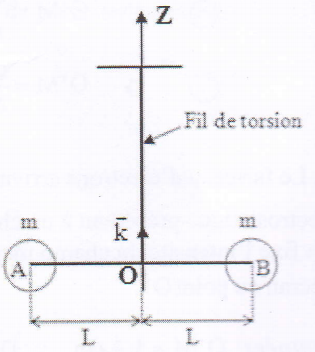
merci de m'expliquer le moment d'inertie de l'ensemble de deux sphères e platine pleines de masse m , de rayon r centrées respectivement en A et B ( la masse de la tige est négligeable)
merci beaucoup
Tu dois savoir que le moment d'inertie d'une boule homogène de masse m et de rayon r par rapport à un de ses diamètre vaut (2/5).m.r2.
Tu dois aussi connaître le théorème de Huygens sur les moments d'inertie...
Je te laisse réfléchir et proposer une solution.
Bonjour Helda,
Intuitivement la réponse est :
(2mL^2) + 2 fois le moment d'inertie de chaque sphère par rapport à son centre, qui est facile à calculer par intégration.
Il doit exister un théorème qui permette de valider cette hypothèse.
à vérifier..
Autrement, le calcul par intégration directe à partir de la géométrie du système entier me paraît compliqué.
Cordialement
Vertigo
Bonjour Vertigo
Pas de problème : les posts croisés sont inévitables...
Et puis, en tenant compte de nos deux réponses complémentaires, handa à la réponse à sa question posée ! 
Je sais l'expression du théorème de Huygens J
Mais je sais pas comment l'appliquer dans ce cas.
Merci de m'expliquer.
Pour la masse de centre B, l'axe perpendiculaire à l'axe de rotation (O,Z) est un axe passant par B et parallèle à (O,Z) que l'on peut noter (B,Z). Cet axe est un axe diamétral pour la boule . Nous avons donc :
Les axes (B,Z) et (O,Z) sont distants de L. Le théorème de Huygens, pour une boule donne :
Reste ensuite à ajouter le moment d'inertie de la boule de centre A mais le raisonnement est analogue.


