Inscription / Connexion Nouveau Sujet
Moment d'inertie
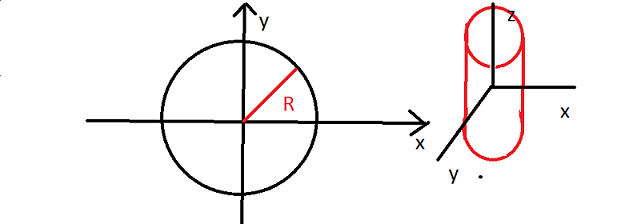
Bonjour, j'ai un petit problème concernant une de mes intégrale en mécanique, pour calculer le moment d'inértie d'un cylindre:
Izz= voici la formule pour calculer le mement en z, cependant, quelque ligne plus loin on trouve : Izz=
Je ne comprend pas comment on peut passer de x²+y² à r² sachant que la variable x=y=r, pour moi on devrais avoir :
Merci de me répondre au plus vite.
bonjour,
quand on écrit: JOz = 

 r2dm
r2dm
r est la distance du point M à l'axe (Oz)
donc en cartésiennes: r2 = x2+y2
oui en cartésiennes x²+y²=r², mais ici, nous sommes passé en coordonnées cylindrique, donc si je comprend bien il est possible d'utiliser les deux en même temps?
par définition:
JOz = 

 d2 dm
d2 dm
où d est la distance du point M à l'axe (Oz)
en cartésiennes: d2 = x2+y2 et dm =  dx dy dz
dx dy dz
en cylindriques: d = r et dm =  r dr dO dz
r dr dO dz
Mais, j'ai un petit probleme, car vous etes d'acord, si on projete r (le rayon), on obtien r*cos(o)+r*sin(o)
avec x=r*cos (o) et y=r*sin(o)
On obtient donc r^2= (r*cos(o) +rsin(o))^2
Ce qui est different de (r*cos (o))^2+(r*sin (o))^2
Je suis donc un peu perdu
Izz=


 r3 dr d
r3 dr d dh[/tex] avec h[-H/2 ; H/2]
dh[/tex] avec h[-H/2 ; H/2]  [0 ; 2
[0 ; 2 ] et r[-R/2 ; R/2]
] et r[-R/2 ; R/2]
en faisant ma triple integrale je tombe sur  (R4/2) 2
(R4/2) 2 h et enfin je tombe sur mR2
h et enfin je tombe sur mR2
alors que je devrais trouvez (mR2)/2
pour balayer tous les points M du cercle UNE SEULE FOIS il faut faire varier  entre O et 2pi et r entre O et R
entre O et 2pi et r entre O et R
si tu prends  entre O et 2pi et r entre -R et R tu balayes 2 fois chaque point M
entre O et 2pi et r entre -R et R tu balayes 2 fois chaque point M

 + r*sin(o)
+ r*sin(o)  (relation VECTORIELLE)
(relation VECTORIELLE)
 r*cos (o) + r*sin(o)
r*cos (o) + r*sin(o) (x2+y2)
(x2+y2)