Inscription / Connexion Nouveau Sujet
Moment cinétique d'un système
Bonjour.
Je n'arrive pas à trouver la bonne solution d'un problème de mécanique :
Un système tourne selon un cercle horizontale.
On sait que la tension du fil horizontale est de 8366 N, la masse du système (la personne) est de 110kg.
Il faut montrer que le moment du système par rapport au centre de l'orbite circulaire est égale à 20700 Js.
En plaçant le centre de l'orbite sur l'axe horizontale, je trouve un moment égale à 0.
En placant le centre de l'orbite (point O) au niveau de la flèche, je trouve la sommes des moments égale = (-l*mg*sin (teta) - l*T*cos(teta) )ez (selon l'axe Z)
avec l = d / cos (teta) ( c'est la longueur du cable diagonal)
LA photo :
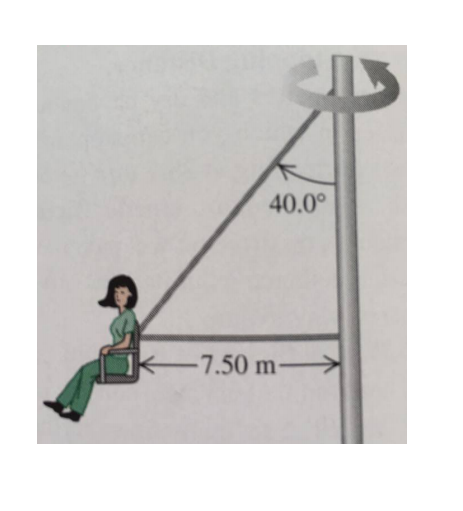
Bonjour
Un peu toujours la même chose. L'application de la relation fondamentale de la dynamique à la personne assimilée à un point matériel conduit à :
(notation déjà utilisée).
Sachant que , tu peux déterminer la norme du vecteur vitesse. Ensuite, il te suffit d'appliquer la formule de définition du moment cinétique au centre O de la trajectoire...
Merci pour votre réponse,
Mais où se situe le centre O de la trajectoire ? (moi je l'aurais placé sur l'axe horizontale)
Et comment avez vous trouvé que tan(alpha) = a/g ?
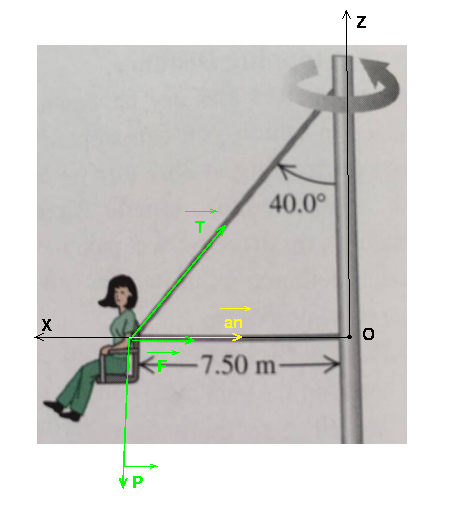
Oublie mon message précédent : j'ai commis l'étourderie de négliger la force exercée par la tige horizontale. J'imagine de l'ensemble(personne+siège) de masse m=110kg est soumise, dans le repère terrestre supposée galiléen, à trois forces :
- son poids P vertical descendant égal à m.g
- la tension T de la tige inclinée d'intensité T inconnue
- la force F exercée par la tige horizontale d'intensité F=8366N.
L'accélération est normale centripète : an=v2/R avec R=7,50m.
Il te faut alors projeter la relation fondamentale sur les deux axes, ce qui te permettra d'obtenir v.
Tu parles de moment du système. Cela n'a pas de sens. Compte tenu de l'unité fournie, je pense qu'il s'agit du moment cinétique du système calculé au point O centre de la trajectoire circulaire (voir figure). Il ne s'agit pas du moment des forces mesuré en N.m !
Quelle définition du moment cinétique en un point as-tu exactement ?
Tu devrais logiquement obtenir
m.v.R
Merci pour la formule, c'est bien ça, cependant, je n'ai pas compris comment on obtient cette formule (ou bien c'est une formule à apprendre par coeur ? )
Il ne faut surtout pas confondre moment cinétique et moment des forces. Dans certains cas le moment des forces est égal à la dérivée par rapport au temps du moment cinétique, pas au moment cinétique !
Pour la définition générale du moment cinétique : as-tu l'habitude d'utiliser le produit vectoriel ?


