Inscription / Connexion Nouveau Sujet
Moment cinétique d'un système
Bonjour,
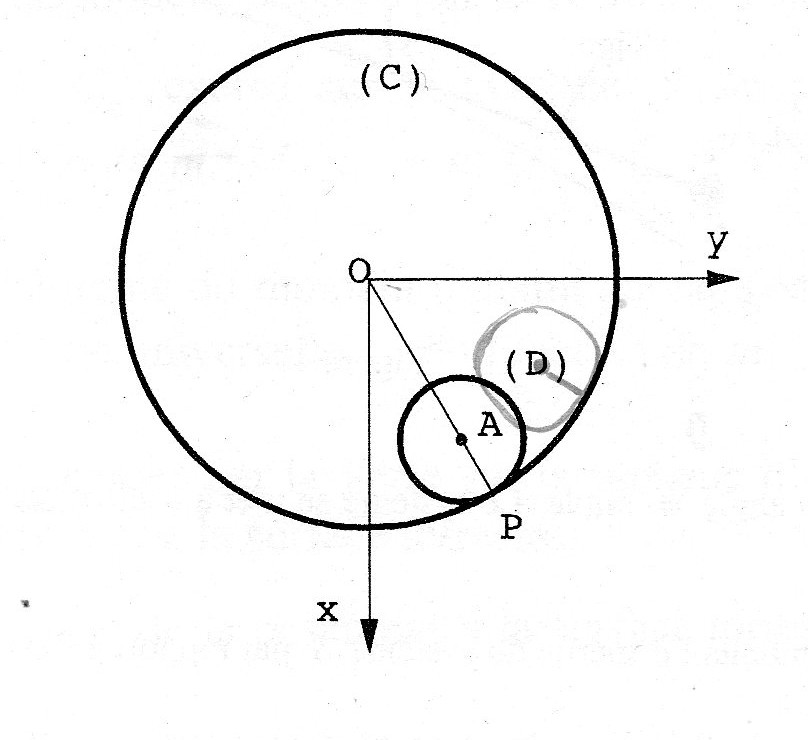
Dans un exercice on me demande de déterminer le moment cinétique d'un système constitué d'un cerceau(C) dans un plan vertical et d'un disque(D) roulant sans glissement à l'intérieur du cerceau.
Je voulais savoir si le moment cinétique de ce système est égale à la somme des moments cinétique de chacun des solides?
Merci d'avance 
Bonsoir,
Je voulais savoir si le moment cinétique de ce système est égale à la somme des moments cinétique de chacun des solides?
La réponse est oui à cette question.
Pour le reste, difficile de t'aider sans plus de précision sur le système... Le cerceau est-il fixe par rapport à la terre qui constitue j'imagine le référentiel d'étude ? Le disque est sans doute homogène...
A priori il faut commencer par établir la condition de roulement sans glissement. Ensuite, plusieurs méthodes sont possibles... Connais-tu les théorèmes de König ?
Peux-tu scanner un schéma du dispositif ?
Merci beaucoup vanoise.J'ai appliqué le théorème de huygens pour avoir le moment du disque en oz et fais la somme avec celui du cerceau est-ce que cele est juste?
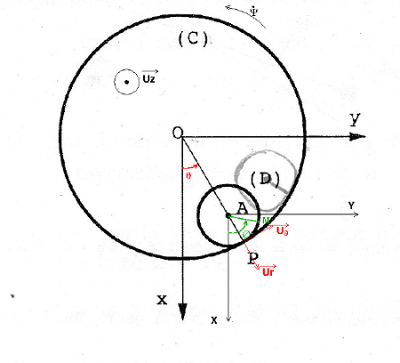
Voici le dessin du système (il ne faut pas prêter attention au cercle gris).
Le mouvement du système est déterminé par  ,
, et
et 
 est l' angle d'un rayon de C avec ox
est l' angle d'un rayon de C avec ox
 est l'angle de OP avec ox
est l'angle de OP avec ox
 est l'angle d'un rayon matériel de D avec ox
est l'angle d'un rayon matériel de D avec ox
OA=a
AP=b
pour la suite de l'exercice on me dit qu'en plus des forces de liaison (le frottement de contact en P est suffisant pour assurer un roulement sans glissement,mais on néglige le couple de résistance au roulement) le système est soumis à g l'accélération de la pesanteur et à un couple d'axe oz d'intensité  appliqué à C.On demande de former les équations différentielles du mouvement ? Dois je appliquer le théorème des moments cinétiques?
appliqué à C.On demande de former les équations différentielles du mouvement ? Dois je appliquer le théorème des moments cinétiques?
Ici la condition de roulement sans glissement est bien  point*a=-b*(
point*a=-b*( point+
point+ point)?
point)?
Je ne suis pas sûr d'avoir bien compris tes notations. Le schéma avec les définitions et les orientations des angles aurait été plus clair.
Ce que tu notes  point représente bien la vitesse angulaire de (C) par rapport à la terre ? Si oui, la vitesse de P, considéré comme appartenant à (C) s'écrit : (a+b)
point représente bien la vitesse angulaire de (C) par rapport à la terre ? Si oui, la vitesse de P, considéré comme appartenant à (C) s'écrit : (a+b) point et non a.
point et non a. point. (vitesse mesurée par rapport à la terre).
point. (vitesse mesurée par rapport à la terre).
Pour obtenir la vitesse de P, considéré comme appartenant à (D), tu peux appliquer la relation classique concernant la distribution des vitesses dans un solide. En notant  point la vitesse angulaire de OA par rapport à la terre et
point la vitesse angulaire de OA par rapport à la terre et  point (pas plutôt
point (pas plutôt  point ?) la vitesse angulaire de (D) par rapport à la terre, cette relation conduit à une vitesse de P par rapport à la terre égale à :
point ?) la vitesse angulaire de (D) par rapport à la terre, cette relation conduit à une vitesse de P par rapport à la terre égale à :
a. point+b.
point+b. point.
point.
D'où la relation :
Tu peux vérifier que ce résultat est cohérent avec le cas simple où (C) est immobile par rapport à la terre ; alors :
Attention : ce que je viens d'écrire est peut-être faux, si je n'ai pas bien interprété les symboles fournis et compris l'orientation des angles. Je les ai tous supposés orientés dans le sens trigonométrique...
Concernant le moment cinétique de (D) au point O, mesuré par rapport à la terre, l'application du théorème de König conduit directement au résultat sans avoir à passer par le théorème de Huyghens mais ce théorème n'est peut-être pas à ton programme...
C'est le seul schéma fournit et c'est cela mon problème car j'ai du mal à analyser les données. Ton raisonnement semble cohérent mais quel rapport avec le roulement sas glissement du coup?
Si les théorèmes de Koenig sont au programme mais comme nous faisons pas d'exercices d'application en cours je ne sais vraiment quand l'utiliser.
Bonjour
quel rapport avec le roulement sas glissement du coup
J'ai écris que la vitesse de P considéré comme appartenant à (C) :
Pour la suite, dans la mesure où la force de frottement en P ne consomme pas de puissance, je me demande si le plus simple ne consisterait pas à utiliser le théorème de l'énergie puissance, c'est à dire le théorème de l'énergie mécanique classique dérivé par rapport au temps :
Pour le système {(C)+((D)}, la dérivée par rapport au temps de la somme (énergie cinétique + énergie potentielle de pesanteur) est égale à la puissance instantanée du couple dont tu connais le moment... Etude faite bien sûr dans le référentiel terrestre.
Le théorème du moment dynamique peut aussi être utilisé... Dans les deux cas, un théorème de König intervient...
Bonjour,
Oui je comprend d'ailleurs en refaisant mon raisonnement j'en viens au même résultat mais avec un facteur - devant  je pense que vu qu'on ne connait pas la direction de la rotation ce n'est pas important.
je pense que vu qu'on ne connait pas la direction de la rotation ce n'est pas important.
En fait j'ai utilisé le théorème de hyugens car on vous donne le moment d'inertie des solides dans l'énoncé(désolé j'ai oublié de le préciser) d'ailleurs pour le moment de D en oz je trouve J( point+
point+ point)+ma² est-ce correct?
point)+ma² est-ce correct?
Bonsoir,
Puisque tu dis que les théorèmes de Kônig sont à ton programme mais que tu n'as pas l'habitude de les utiliser, les voici appliqués à ce problème.
Soir R : (Oxyz) le repère terrestre supposé galiléen. Le repère RA : (Axyz) est le repère "barycentrique" du solide (D) : son origine est le centre d'inertie du solide et ses axes sont constamment parallèles aux axes du repère R. Le théorème de König concernant le moment cinétique du solide (D) calculé au point O dans le repère R, s'écrit :
Le moment cinétique en O, mesuré dans le repère R est le moment cinétique en A mesuré dans le repère RA auquel on ajoute le moment cinétique en O, mesuré dans R du centre d'inertie A affecté de la masse totale du solide. Le mouvement barycentrique de (D) est une rotation autour de l'axe Az à la vitesse angulaire .
Pour l'énergie cinétique de (D) mesurée dans (R), le théorème de König s'écrit :
L'énergie cinétique de (D) mesurée dans (R) est égale à l'énergie cinétique de (D) mesurée dans (RA) augmentée de l'énergie cinétique du point A affectée de la masse totale du solide.
Si (D) est un disque homogène :