Inscription / Connexion Nouveau Sujet
moment cinétique d'u solide.
Bonjour,
voilà j'ai un problème avec un devoir. Voici l'énoncé :
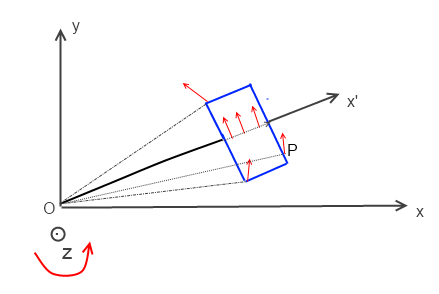
Un demi disque (S) est lié en C à l'extrémité d'ue tige OC de longueur L et de masse négligeable. Cette tige tourne autrour de l'axe Oz avec une vitesse constante en restant dans le plan xOy ( voir figure ). Le plan de (S) reste vertical et constamment perpendiculaire à OC confondu avec Ox'.
On admettra que le torseur des actions de contact s'exerçant en C a comme éléments de réduction en C en projection dans R' ( C,x',y',z') :
a) Rx'; Ry'; Rz'
b) 0x' ; My' ; Mz'
On note :
1°)
Calculer , vitesse de G par rapport à R, en projection sur R'.( j'ai résolu cette question ).
2°)
Voici la question qui me pose problème.
Donner les composantes sur les axes de R' du moment cinétique en G de (S) relatif au repère R.
Indications :
Dans une question précédente on nous a fait calculer la matrice d'inertie en G relative aux axes Gx', Gy', Gz'. Matrice JG diagonale dont les éléments diagonaux s'écrivent I1, I2 et I3, et que j'ai calculé.
Cela fait plusieurs jours que je cherche, sans succès.
Comment faire ?
Je vous remercie par avance. 
Bonjour,
bien sûr.....mais justement le problème est que le mouvement n'est pas plan et que d'autrepart la matrice d'inertie dans le théorème de Koenig est celle calculée dans le repère R* ( barycentrique ) alors qu'ici on nous a fait calculer cette matrice dans le repère R'.
Ou je me trompe ?
bonjour,
la matrice d'inertie dans le théorème de Koenig est celle calculée dans le repère R* ( barycentrique ) alors qu'ici on nous a fait calculer cette matrice dans le repère R'.
il faut utiliser le théorème de Huygens:
http://scienc.industrielles.free.fr/S2I%20en%20PSI/nouveausite/mecanique/pdf/huygens.pdf
Bonjour,
d'abord merci de votre réponse. Mais il reste un petit problème. Les axes de R*( barycentrique ) et R' ne sont pas du tout parallèles ( voir figure ) donc je ne vois pas comment appliquer Huygens...à moins qu'il existe un autre théorème de Huygens permetant de passer de R' à R*, théorème qui n'est pas dans mon cours.
D'autre part le lien ne fonctionne pas.
Merci encore.
PS : Le problème a été posé en 1980 aux ENSI.
Dans une question précédente on nous a fait calculer la matrice d'inertie en G relative aux axes Gx', Gy', Gz'. Matrice JG diagonale dont les éléments diagonaux s'écrivent I1, I2 et I3,
donc tu as la matrice d'inertie du solide en G exprimée dans R' (lié au solide)
 G* = JG
G* = JG  (S)/R
(S)/R
mais tu as le droit d'utiliser R' comme base de projection donc d'exprimer JG et
 dans R'
dans R'
pour JG c'est fait, il te reste à exprimer
 (S)/R dans R' et tu trouves
(S)/R dans R' et tu trouves  G* exprimé dans R'
G* exprimé dans R'
sauf erreur
Hello krinn,
oui oui je m'intérroge effectivement car dans la formule du cours :
( exprimée dans R')
le n'est pas celui qu'on nous a fait calculer. Ce
de la formule doit être la matrice d'inertie calculée dans le repère barycentrique (G,x,y,z), or celui qu'on nous a fait calculer
dans une question précédente l'a été dans (G,x',y',z') qui n'est pas du tout le repère barycentrique.
Mais tu as peut-être raison....il y a quelque chose qui m'échappe. 

En tout cas merci encore une fois. 
quand on écrit :  * =
* =  G/R = JG
G/R = JG  (S) / R
(S) / R
on a le droit de calculer JG et  (S) / R dans la base que l'on veut
(S) / R dans la base que l'on veut
(car un vecteur peut s'exprimer dans plusieurs bases, de même pour J)
et on s'arrange normalement pour que les coeff de la matrice d'inertie soient constants, donc on prend en général un repère lié au solide comme base (ici R') , et non pas R*
mais il n'empêche que tu calcules  G/R mais exprimé dans une base qui n'est pas R, ni R* mais R' (dans cet exo)
G/R mais exprimé dans une base qui n'est pas R, ni R* mais R' (dans cet exo)
Bonjour krinn,
effectivement je viens de comprendre mon incompréhension  . En fait JGR' c'est JGR exprimée dans R'. C'est sur ce point que j'avais du mal. En fait on calcule par rapport à R mais on projète dans R'. Maintenant c'est OK.
. En fait JGR' c'est JGR exprimée dans R'. C'est sur ce point que j'avais du mal. En fait on calcule par rapport à R mais on projète dans R'. Maintenant c'est OK.
Merci de tes explications. 
Bonjour,
j'ai un petit problème  pour calculer la vitesse du centre de gravité dans R ( mais exprimée ) dans R', dans le cas suivant :
pour calculer la vitesse du centre de gravité dans R ( mais exprimée ) dans R', dans le cas suivant :
"Un demi disque (D) est lié en C à l'extrémité d'ue tige OC de longueur L et de masse négligeable. Cette tige tourne autrour de l'axe Oz avec une vitesse constante en restant dans le plan xOy ( voir figure ). Le plan de (S) reste vertical et constamment perpendiculaire à OC confondu avec Ox'." (Voir figure).
En fait je trouve deux résultats différents selon la méthode de calcul.
a) dérivation de
b) composition des vitesses.
J'ai l'impression que a) n'est pas valable ( j'ai comme le sentiment que la composante de la vitesse sur x' est nulle. ) mais n'en suis pas très sûr.
Merci d'avance pour vos explications. 
*** message déplacé ***
bonjour,
je trouve:
V G/R = -d 'sin
'sin x' +(d
' +L
 'cos
'cos) y' -L
 'sin
'sin z'
tu as dû te tromper dans la composition des vitesses:
la vitesse relative par rapport à R1 est le terme d'y'
la vitesse d'entraînement c'est le reste 
sauf erreur
Bonjour Krinn,
oui effectivement pour la réponse a) je me suis trompé en retranscrivant. La composante sur est bien :
avec
Bon, donc contrairement à mon "intuition", c'est donc bien la a) ( rectifiée ) qui est la bonne répnse. Merci Krinn. 
A Coll :
oui désolé. 
ton intuition est fausse car G est désaxé par rapport au plan (Cx'z)
le champ de vitesse d'un corps en rotation autour d'un axe fixe Oz est le suivant: (cf figure)
seuls les points dans le plan (O,x'z) ont une vitesse nulle selon x' mais les autres ont une composant sur x' car
V(P) =  ^ OP (qui est normal à OP, pas à x'
^ OP (qui est normal à OP, pas à x'

 , où J=
, où J= r²dm
r²dm
