Bonjour DrPB,

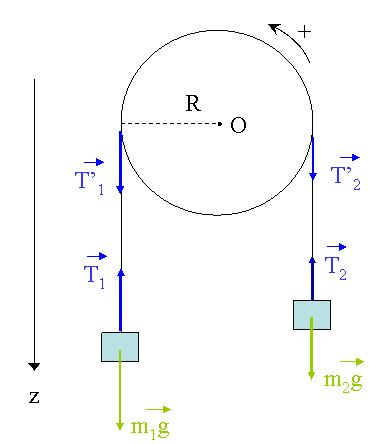
tu aurais du detailler tes calculs dans ton post, j'aurais alors pu voir ou etait ton erreur. Du coup, je te propose le mien, a suivre avec la figure ci-dessous :

J'appelle m₁ et m₂ les masses accrochees a la poulie de rayon R et de masse m. Je suppose que m1 > m2, donc m1 va descendre, m2 va monter et poulie va tourner dans le sens trigo. Je choisis un axe Oz vertical et oriente vers le bas, cad dans le meme sens que le mouvement de m1 et donc compatible avec le sens positif de rotation de la poulie.

J'appelle T₁ et T'₁ les tensions du fil de gauche (T₁ au niveau de la masse m1 et T'₁ au niveau de la poulie), T₂ et T'₂ idem pour le fil qui supporte la masse m₂. Les vecteurs sont ici notes en gras. On a bien sur T'₁ = - T₁ et T'₂ = - T₂ ; j'appelle donc T₁ le module commun aux forces T₁ et T'₁, et T₂ le module commun aux forces T₂ et T'₂.
Par ailleurs, je note a₁ = d²z/dt² = a l'acceleration de la masse m₁, et a₂ celle de la masse m₂ ; on a evidemment a₂ = - a, et a est l'acceleration tangentielle demandee dans ton enonce si le fil ne glisse pas dans la gorge de la poulie.

Alors voici mes equations, projetees sur l'axe Oz pour celles qui probviennent de la 2ieme loi de newton (PFD), et sur un axe perpendiculaire a ton ecran et venant vers toi pour la relation issue du theoreme du moment cinetique :

m₁g - T₁ = m₁a, m₂g - T₂ = -m₂a (PFD) ;
T₁ - T₂ = J.d²/dt² (theoreme du moment cinetique) ;
J = mR²/2 (poulie = cylindre plein) ;
d²/dt² = a/R (relation entre l'acceleration angulaire de la poulie et l'acceleration lineaire de m₁, lorsque le fil ne glisse pas sur la poulie).

Bon, avec tout ca on obtient facilement l'expression de l'acceleration a :

a = (m₁ - m₂).g / (m₁ + m₂ + J/R²) = (m₁ - m₂).g / (m₁ + m₂ + m/2) avec J/R² = m/2.

Application a ton exercice :
c'et la masse la plus lourde qui est egale a celle de la poulie, donc je suis oblige de modifier les notations de ton enonce : je pose m₁ = m, et m₂ = m/2. La relation que j'ai obtenue donne alors a = g/4.

Si tu as des pb de comprehension n'hesite pas a mettre u post.

Prbebo.

  D'abord un grand merci pour ta réponse bien détaillée, mais à dire je ne comprend pas trop lorsque tu introduit le théorème du moment cinétique, est-ce bien ça où pas plutôt le moment de force qui serait donc:

(T1-T2).R=J.(la dérivé seconde de teta/ désolé je sais pas comment l'écrire là dessus)

C'est à dire que je ne comprend pas pourquoi on ne multiplie pas par le rayon R. Où alors le moment cinétique n'est pas:

L=J.(vitesse angulaire)=m.R.v ?

Merci DrPB.

Ah oui, bien sur, il faut ecrire (T₁ - T₂).R = J.d²/dt², ce qui avec d²/dt² = a/R donne bien T₁ - T₂ = a/R². Desole pour l'oubli, mais le reste de mom corrige tient la route.

Prbebo.

Oui maintenant c'est bon, merci beaucoup de ton aide Prbebo.