Bonsoir
As-tu fourni un énoncé complet ? Quelle est la relation entre le modèle de Van der Walls et la détente de la vapeur d'eau ?

Le premier tableau te fournit les paramètres (U,T,V) de l'état initial.
A l'aide d'un tableur ou d'un logiciel scientifique quelconque, tu peux modéliser l'isobare P=70bar représentant les variations de T en fonction de V. Une régression polynomiale de degré 2 suffit au niveau de la précision. Puisque tu connais VF=Vi, tu obtiens TF.

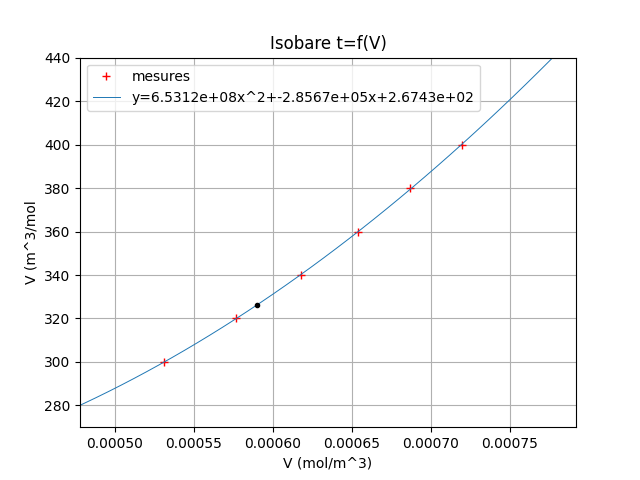
Pour illustrer mon message précédent, voici tracée l'isobare t=f(V) pour P=70bar. Les croix rouges correspondent aux points fournis par le tableau n° 2. En bleu, la branche de parabole dont l'équation est calculée par le programme informatique pour passer au plus près des différents points. Le volume initial étant connu : Vi=5,90.10^-4m³/mol, il suffit de déterminer la température correspondante. L'état final correspond au point noir sur la courbe.
Pour l'énergie interne : méthode analogue en traçant la courbe U=f(V) pour P=70bar.

Bonjour,

Juste une remarque : on peut peut-être se contenter d'une interpolation, donc faisable avec une calculatrice 4 opérations.

Bonjour gts2
Pourquoi pas ? A condition tout de même de placer les points de coordonnées (t,V) dans un repère pour s'assurer que la courbe est bien, avec une approximation raisonnable, assimilable à un segment de droite sur l'intervalle  320<t<340 (en °C).

Je vous remercie pour votre réponse. En fait, l'exercice revient à trouver la température finale sachant que le volume molaire reste le même tout au long de l'expérience.

Mais j'ai une question, si l'on connaît effectivement le volume molaire initial et final (), si j'utilise l'équation de Van der Walls, alors je trouve T=589K et non 599K comme la correction et vous trouvez.

Je voulais savoir si c'était dû à une imprécision de la régression linéaire ou si mon raisonnement n'était pas le bon.

Les tableaux fournis sont des extraits de tables thermodynamiques a priori très fiables alors que l'équation  de Van der Waals n'est qu'une modélisation, assez bien adaptée à la description des propriétés d'un gaz au voisinage des conditions critiques mais évidemment moins fiables que des mesures dans le contexte de cette expérience. Cela d'autant plus que les coefficients a et b que tu obtiens ne semblent pas tout à fait correspondre à de la vapeur d'eau.
Autre remarque : je ne sais pas si cela est demandé quelque part dans ce problème mais il serait intéressant de comparer les résultats obtenus ici à partir des tables thermodynamiques avec ceux qui correspondraient à un gaz parfait.

Bonjour,

J'ai trouvé un sujet proche de celui-ci et dans ce sujet, après avoir calculé a et b à partir d'un point du tableau, on demandait de vérifier avec un autre point et de conclure sur la fiabilité de Van der Waals. Vous n'avez pas dans la première partie, une question de ce type ?

Je vais vous répondre à tous les deux :

Oui, la 1ère partie de l'exercice concerne la validité ou non du modèle de Van der Walls.

En utilisant la relation de VdW, pour une pression de et un volume de ,

On trouve Soit une erreur relative de 1 % par rapport à la valeur exacte ()

Quant à l'énergie interne du modèle de VdW, donnée par la relation : , on fait la différence avec le cas où



Alors soit 0,001 % de différence avec la valeur exacte.

Donc le modèle du gaz réel de Van der Walls est valide.

Aussi, il ne s'agit pas d'un gaz parfait car la température étant constante, d'après la 1ère loi de Joule, l'énergie interne devrait être constante.

Merci pour vos réponses , je ne pense pas que j'aurais pensé à utiliser la régression linéaire.

Attention tout de même : les calculs demandés peuvent donner une image exagérément optimiste du modèle de Van der Waals. Je ne sais pas comment ont été obtenues les valeurs des constantes a et b : sans doute à partir des valeurs de P, T et V appartenant au domaine  de valeurs faisant l'objet de cette étude.
Imaginons que l'on veuille déduire de ce modèles les valeurs critiques de P, T et V. On serait en total désaccord avec l'expérience. En effet, selon les tables thermodynamiques, les valeurs de a et b déduites des valeurs critiques de P, T et V sont :
a=0,5537J.m^-3.mol^-1
b=3,05.10^-5m³/mol
Valeurs assez différentes des tiennes.

Vos informations sont très intéressantes.

En fait il est demandé dans l'énoncé de l'exercice de calculer les valeurs de a et b de façons particulières :

La valeur de en utilisant la variation d'énergie interne entre les états et . Aussi, est calculé en utilisant l'équation d'état à .

Les valeurs de mon premier message sont celles que j'ai trouvées et la correction de l'exercice indique les mêmes valeurs.

Enfin, je suis curieux de savoir à quoi correspond la valeur critique dont vous parlez.

Merci pour ton dernier message qui confirme mon message précédent sur le domaine de validité de ton équation de Van der Waals.
Tu auras sans doute l'occasion d'étudier en détail la notion de condition critique quand tu étudieras les changements d'état et en particulier les liquéfactions et vaporisations. Disons simplement que la température critique d'un corps pur est la valeur Tc au de-dessus de laquelle il est impossible de liquéfier un gaz par compression isotherme. La pression critique Pc est la pression au-dessus de laquelle il est impossible de liquéfier un gaz par refroidissement isobare. Exemple tiré de la vie courante concernant deux gaz utilisés pour le chauffage : le butane et le méthane. Pour le butane : Tc=150,8°C ; il est donc tout à fait possible de liquéfier du butane par compression à température ambiante. Le butane est commercialisé à l'état liquide dans des bouteilles à température ambiante mais pression élevée. Pour le méthane : Tc=-82,6°C. Il est possible de transporter le méthane dans des méthaniers à l'état liquide mais les cuves doivent être maintenues à température inférieure à Tc : cela est coûteux. C'est pour cette raison que le méthane est essentiellement distribué à l'état gazeux dans des canalisations (gazoducs).
Au niveau théorique, dans le diagramme de Clapeyron, l'isotherme critique (T=Tc=constante) présente un point d'inflexion avec tangente horizontale au point critique de coordonnées Pc,Vc (volume molaire critique). Cela se traduit mathématiquement par les deux égalités :



Cela permet d'obtenir les valeurs de a et b. Voir calculs sur ce document :

Eh bien merci pour toutes vos réponses, votre site est vraiment très utile en plus d'être agréable.

Bon week end, François.