Bonjour a tous, voici un exercice sur un noyau en rotation dans un modèle de goutte. J'ai réussi à faire la première question seulement après je bloque. Si quelqu'un pouvait m'aider cela m'arrangerai bien. Je vous remercie par avance pour vos réponse.

Le but de cette question est d'examiner quelle est la forme d'un noyau à très grand moment cinétique et l'énergie la plus basse possible. De manière a simplifier les calculs, on supposera que le noyau est un cylindre homogène, de densité uniforme, incompressible et on ne tiendra pas compte des effets colombiens. On envisagera la rotation du noyau soit autour de l'axe ,axe symétrie du cylindre, soit autour de l'axe axe perpendiculaire à et passant par le centre 0 du noyau.
Les moments d'inertie du noyau par rapport à ces deux axes seront pris égaux à :


On rappelle que l'énergie de rotation d'un système de moment cinétique autour de l'axe D vaut ou est le moment d'inertie du système par rapport à l'axe D.

1. Ecrire, pour chacune des deux rotations possibles autour des axes et   et en fonction des variables et , l'énergie du noyau sous la forme

en supposant que le noyau à un moment cinétique L par rapport à l'axe considéré. Les contributions et sont respectivement proportionnelle au volume et à la surface du noyau que l'on exprimera en fonction des variables et . Préciser le signe de ces contributions :
et

donc pour l'axe
E= + +
pour l'axe
E= + +

2. Ecrire les relations que doivent vérifier et   pour que l'énergie E soit minimale. On notera l'énergie correspondante.

3. En déduire que = quand L=0.

4. Montrer que si la rotation s'effectue autour de ,   augmente avec L. Est-ce surprenant ?

5. Montrer que si la rotation s'effectue autour de ,   augmente avec L. Est-ce surprenant ?

6. On se place à L grand. Expliquer la dépendance de L de l'énergie minimum :
- dans le cas d'une rotation de
- dans le cas d'une rotation de

7. En déduire la forme d'équilibre la plus stable d'un noyau à grand moment angulaire.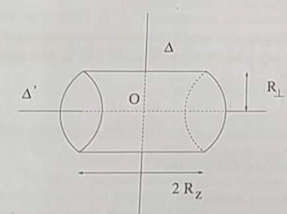



_{* mmalou > gabriel78, peux-tu renseigner  ton profil conformément à  FAQ Q12 [lien] *}