Inscription / Connexion Nouveau Sujet
Mobile entre deux ressorts
Bonjour, j'ai un soucis avec l'exercice dont voici l'énoncé
Référentiel supposé Galiléen. Un point matériel M de masse m est attaché à deux ressorts (1) et (2) horizontaux de raideurs k1 et k2 et de longueurs à vide l01 et l02 reliés à deux points fixes A et B distan de (l01+l02).
Le point M glisse sans frottemen le long de l'axe (Ox) à partir de sa position d'équilibre O. Il est repéré sur cet axe par son abscisses x=OM
Je dois établir l'équation différentielle du mouvement de M. Je note l1 la longueur du ressort (1) à l'instant t et l2 la longueur du ressort (2) à l'instant t.
Donc j'ai commencé par appliquer le principe fondamental de la dynamique sur l'axe (Ox), ce qui me donne
m*x" = -k1(l1-l01) - k2(l2-l02)
et en fait je n'arrive pas à aller plus loin... Déjà je ne vois pas à quoi correspond x(t) ? x(t)=l2-l1 ?
merci d'avance
bonjour,
il suffit de faire un dessin:
en M de combien s'est allongé le ressort (1)?
même question pour le (2)
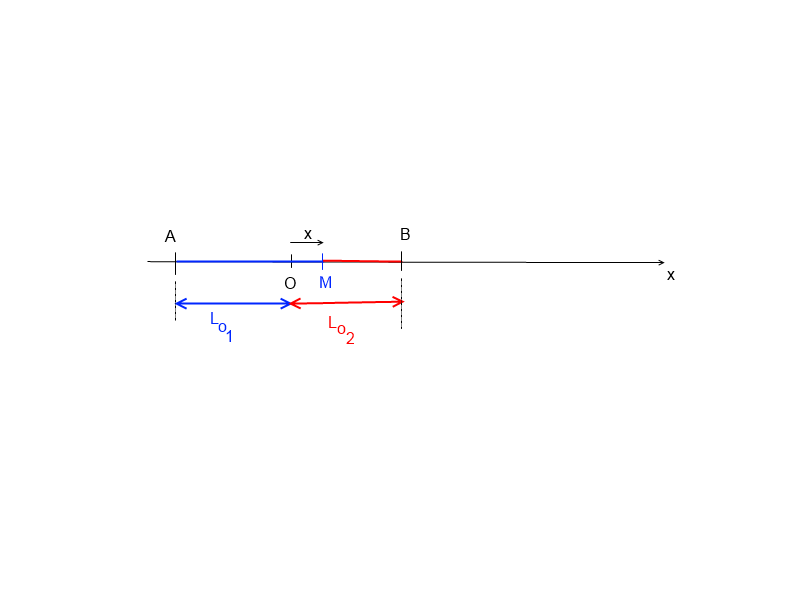
Alors en M le ressort (1) s'allonge de l01 + OM et (2) s'allonge de l02 - OM
C'est bien ça ? Du coup j'aurais x(t)= l01 + OM + l02 - OM = l01+l02 ? Mais vu que x dépend de t cela ne peut pas être ça...
Bonjour,
Le schéma fourni par Krinn est parfaitement clair ! À l'instant de date t donné, correspondant au schéma, de combien est allongé le ressort n° 1, de combien est raccourci le ressort n° 2 ? Quelles sont les expressions des vecteurs forces exercées par les ressorts sur l'objet de masse m. Vérifie que la relation est bien algébrique, c'est à dire qu'elle s'applique quel que soit le signe de x.
Je te laisse réfléchir...
Tu devrais aboutir à une équation différentielle de la forme :
Alors en M le ressort (1) s'allonge de l01 + OM et (2) s'allonge de l02 - OM
C'est bien ça ? Du coup j'aurais x(t)= l01 + OM + l02 - OM = l01+l02 ? Mais vu que x dépend de t cela ne peut pas être ça.
pourtant ça m'avait l'air d'être clair sur mon beau dessin

quand l'extrémité des ressorts se déplace de O à M:
la longueur du ressort(1) passe de: Lo1 à Lo1 + x donc l'allongement du ressort(1) vaut ...
la longueur du ressort(2) passe de: Lo2 à Lo2 - x donc l'allongement du ressort(2) vaut ...
il faut bien distinguer longueur et allongement
Ahh ok j'ai compris!
l'allongement du ressort(1) vaut Lo1 + OM
l'allongement du ressort(2) vaut Lo2 - OM
merci beaucoup du coup j'ai réussi à trouver l'équation 


