Inscription / Connexion Nouveau Sujet
Miroire de lloyd
Salut tout le monde,
S'il vous plait j'ai besoin de vos aide
Dans ce exercice sur le phénomène d'intérferance avec les miroires de Lloyd (intérferomètre par division du front d'onde), j'ai calculer dans les premiers questions la différance de marche 
, l'ordre d'intérference p, l'intensité I(x) et l'intérfrange i, :
= (2*h*x)/(d+l) + 
/2
p = / = (2*h*x)/(d+l) + 1/2
I(x)=2*I*(1-cos(4
*h*x/( (d+l) ) ) ) (on déduit alors que I(x=0) est manimal, donc une frange centrale sambre)
donc on trouve : i=(d+l)/(2*h)
=632,8 nm
h=1mm
l=30 cm
d=50 cm
La question suivante demande de déterminer le nombre N de frange que l'on peut observer sur l'écran, Nble nombre de franges brillantes et Ns le
nombre de franges sombres .
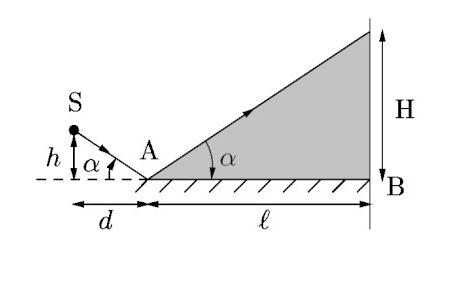
J'ai commencer par déterminer H ( en calculant sin(
) par 2 méthodes ), on trouve alors H= l*h/d, le nombre de franges qu'on peut observer est alors N=H/i, l'application numérique donne N=2,3 . donc on obesrve environ 2 franges, une brillante et l'autre sombre ! Alors que dans la correction, je trouve qu'on doit observer 5 franges, 2 brillantes et 3 sombres !
Pouvez vous m'aider s'il vous plait,
Merci infiniment
Bonsoir
Ta méthode ne donne pas toujours le bon résultat pour le nombre de franges. Il faut partir de la frange centrale puis voir ce qui se passe de chaque côté.
Merci beaucoup pour votre réponse
Sauf que j'ai pas bien compris, j'ai vraiment essayer plusieurs fois de refaire le shéma et de chercher une autre méthode, mais sans y parvenir .
Merci à vous
Se limiter à calculer le rapport (largeur du champ d'interférence)/interfrange n'est pas suffisant pour bien comprendre. Il faut partir de la frange x=0 et voir se qui se passe de chaque côté. Évidemment ici, la situation est simplifiée car les valeur de x négatives n'ont pas de sens physique.
x=0 correspond à p=1/2 donc x=0 correspond à une frange sombre.
Les autres franges sombres seront en x=k.i avec k entier positif.
Puisque H/i=2,37, les valeurs possible de k sont 1 et 2.
On obtient bien 3 franges sombres.
Les franges brillantes correspondent à x=i/2 +k'.i=(k'+1/2)i où k' est un entier positif.
Les seules valeurs possibles de x sont : x=i/2 et x=1,5.i
Tu obtient seulement 2 franges brillantes.
Imagine que tu ais obtenu : H/i=2.65 : tu aurais obtenu 3 franges brillantes et trois sombres.
Annuler
connectez vous