Inscription / Connexion Nouveau Sujet
Miroir de Lloyd
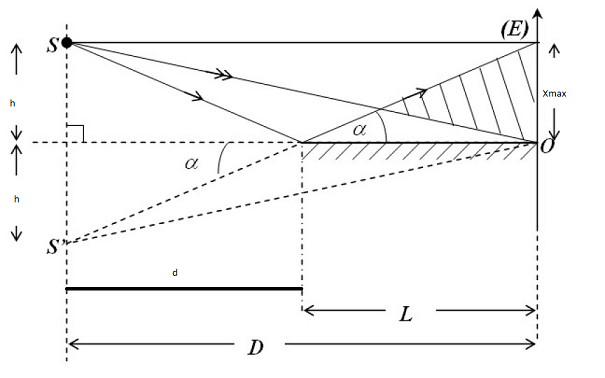
Un miroir plan de longueur L = 10cm est éclairé sous une incidence rasante par une source ponctuelle et monochromatique S (λ0 = 0.546µm) placée à une faible distance h = 1mm au-dessus du plan du miroir et à une distance d = 20cm en avant de celui-ci.
(a) En un point P de l'écran, quels sont les deux rayons qui interfèrent?
(b) Déterminer la position du point S0 d'où semblent provenir tous les rayons issus de S se réfléchissant sur le miroir.
(c) En exploitant ce point, montrer que la différence de marche entre deux rayons interférant en P a pour expression δ = 2axP/(L + d). Le miroir introduit un déphasage de π, ainsi le retard de phase du rayon réfléchi par rapport au rayon direct en P s'écrit ϕ = 2πδ/λ0 + π.
(d) Onconsidèrel'amplitudedesvibrationségalesen P pourlesdeuxondes.Exprimerl'intensitélumineuse en P en fonction de λ0, d, L, h et xP.
(e) Observera-t-on en x = 0 une frange brillante ou sombre?
(f) Représenter la zone d'interférence sur l'écran. On note xmax l'abscisse du maximum de cette zone.
(g) Déterminer l'ordre d'interférence pour xP = xmax.
(h) En déduire le nombre de franges brillantes observées.
Bonjour a tous, je ne vois pas comment calculer xmax a la question (g) est ce qu'on pourrais m'aider stp
Bonjour,
je ne vois pas comment calculer xmax a la question (g)
Le théorème de Thalès peut se révéler utile...
Oui exactement, j'ai calculé xmax, j'ai trouvé qu'il vallait 10cm et que sur votre schéma E peut être considéré comme étant sur O
Après avoir fait le calcul avec cette valeur je trouve p=1221001,22 ce qui me semble complètement faux
Pour trouver xmax j'ai fais pythagore afin de trouvé SA ( À étant le point ou commence le miroir )et donc trouver l'angle (SAB) avec B le milieu de SS', le cos de l'angle=0
Or (SAB)=(OAE) donc E est sur 0
Bonsoir,
Si tu prends les deux triangles rectangles "opposés par le sommet" d'angles au sommet 
, tu peux écrire, d'après le théorème de Thalès :
La suite semble "classique"
OK pour xmax. En revanche revois ton calcul de l'ordre d'interférence (erreur de puissance de 10 selon moi) et n'oublie pas que la frange d'ordre nul est noire
p=6,1+0,5 = 6,6 à cause du déphasage supplémentaire de 
dû au fait qu'une onde subit une réflexion sur un miroir et pas l'autre...
et du coup il y a 3 franges brillantes ?
Revois bien ton cours ! Les franges brillantes correspondent à des ondes qui interfèrent en phase, c'est à dire lorsque le déphasage
est un multiple de 2. Puisque l'ordre d'interférence est : p=/2, les franges brillantes correspondent à des ordres d'interférence égaux à des nombres entiers.. Il y a donc ici six franges brillantes correspondant à p =1 2 3 4 5 6.
Il aurait aussi été intéressant de dénombrer les franges sombres.
Il y en a 7 correspondant à p = 0,5 1,5 2,5 3,5 4,5 5,5 6,5
Le cas p = 0 est ici impossible : le déphasage minimum n'est pas
=0 mais =/2 pour une raison déjà expliquée dans un message précédent.
Annuler
connectez vous