Inscription / Connexion Nouveau Sujet
Métronome mécanique, moments
Bonjour,
Je suis en difficulté avec un exercice portant sur un métronome mécanique lié à deux ressorts.
Le métronome est configuré ainsi :
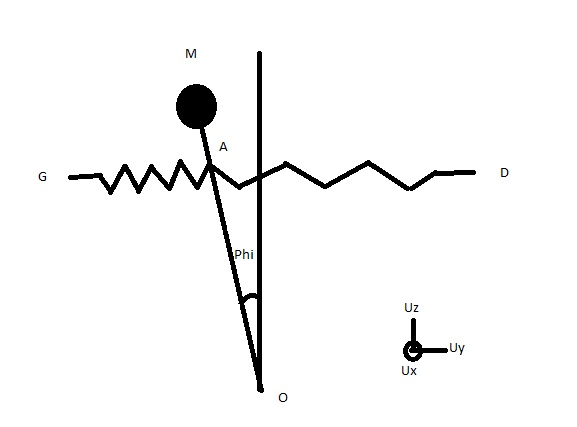
- une tige OM rigide de masse négligeable
- une masse m au point M
- deux ressorts rectilignes identiques GA et AD, longueur à vide lo, raideur k sont attachés en A, A un point de la tige entre O et M à la distance a de O. Le 2ème point d'attache du ressort 1 est G, celui du ressort 2 est D, G(0,-b,a) et D(0, b, a) dans la base cartésienne (o, ux, uy, uz), (a,b)  (
( +)².
+)².
Il n'y a pas de frottements et les oscillations sont dans le plan (0yz).
On considère que les ressorts restent horizontaux comme  petit,
petit,  angle entre la verticale et vecteur OM.
angle entre la verticale et vecteur OM.
Petite précision : le point M est au-dessus de O et non en-dessous.
Pour les forces, il y en a 4 pour le système s = {tige + masse) :
- poids exercé au centre de masse (ici centre de M)
- tension exercée au centre de M
- force du ressort GA exercée en A
- force du ressort AD exercée en A
Il y a ensuite une question très bizarrement formulée disant que la dérivée du moment cinétique par rapport à O d'un système de point Mi est égale à la somme des produits vectoriels des vecteurs OMi par la résultante des forces appliquées en Mi c'est à dire la somme des moments par rapport à O des forces extérieures en M.
Je ne comprends pas comment exprimer le moment des forces par rapport à O pour le système : l'exprimer pour le point centre de M c'est assez simple, pareil pour A. Mais comment ensuite l'exprimer de manière globale ? Additionner les deux moments ?
Il faut ensuite exprimer le moment cinétique par rapport à O du système S dans la base polaire (u , u
, u ) avec u
) avec u vecteur unitaire le long de OM et où (U
vecteur unitaire le long de OM et où (U , U
, U , Ux) est une base orthonormée directe.
, Ux) est une base orthonormée directe.
Je trouve que L S/O = vecteur OM  m*vecteur v = OM*vecteur U
m*vecteur v = OM*vecteur U
 m*vecteur v = m*(OM)²*vecteur U
m*vecteur v = m*(OM)²*vecteur U

 point * vecteur U
point * vecteur U car téta =
car téta =  /2+
/2+ 
Est ce correct ?
Par contre la question suivante me déroute : il faut en déduire ainsi que sin  =
=  comme petit la longueur du ressort GA ! Par quoi dois-je me ramener pour la trouver ? Sans doute au moment de la force...
comme petit la longueur du ressort GA ! Par quoi dois-je me ramener pour la trouver ? Sans doute au moment de la force...
Bonsoir
"Il y a ensuite une question très bizarrement formulée disant que la dérivée du moment cinétique
par rapport à O d'un système de point Mi est égale à la somme des produits vectoriels des vecteurs OMi
par la résultante des forces appliquées en Mi c'est à dire la somme des moments par rapport à O des forces extérieures en M."
Il s'agit du théorème du moment cinétique.
Moment poids = OMxP = r(sin phi Uy + cos phi Uz)x(-mg Uz) = - mgr sin phi Ux
Moment ressordG = OAx(-k(y+b-lo)uy) = OA(sin phi Uy + cos phi Uz)x(-k(y+b-lo)uy) = OAcos phi (y+b-lo) Ux
Par "ressorts rectilignes" j'ai supposé que l'énoncé, dans l'approximation de phi faible implique aucune composante de force de rappel verticale.
Dans ce cas y = OA*tan phi
Moment ressordD = OAx(-k(b-y -lo)uy)
(pas sur de moi pour toutes les expressions rapides)
moment cinétique L = OMxmv
OM = r Ur
solide rigide r=cst
v = r dphi/dt Uphi
L = m r dphi/dt Ux (ce qui me conforme car le mouvement est dans le plan normal à Ux)
"On considère que les ressorts restent horizontaux comme phi petit, phi angle entre la verticale et vecteur OM."
pour phi petit, cos (phi) est proche de 1, sin(phi) est proche de phi et tan phi est aussi proche de phi.
Le théorème du moment cinétique avec dL/dt = m r d^2phi/dt^2 Ux te ferait donc apparaître l'équation différentielle d'un oscillateur harmonique dont la fréquence dépend sans doute de k et de m.. en fait çà devrait aller jusque là pour toi
Bonjour,
je suis sur le même type d'exercice, je m'en sors sauf que je ne parviens pas à déterminer comment on montre que .
C'est une question de trigo, mais je suis embrouillée et n'avance plus depuis des heures.
Je vous remercie par avance de votre aide.