Inscription / Connexion Nouveau Sujet
Mesure du coefficient de frottement solide
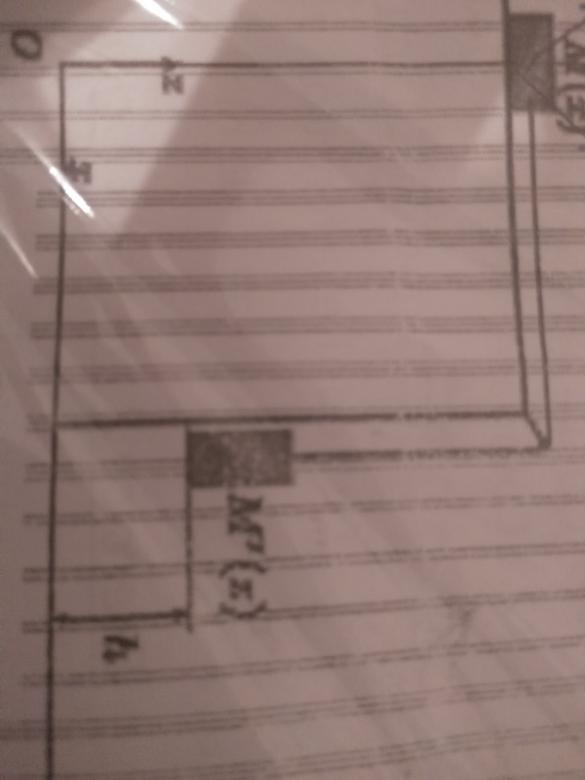
Deux points matériels M et M′, de masse respective m et m′, sont
reliés par un fil inextensible susceptible de glisser sur une poulie
idéale.
Initialement, le fil est tendu et le point M repose sur un support,
à une hauteur h du sol. A l'instant t = 0, on enlève le support,
le point M′ descend, et le point M se met à glisser sur le plan
horizontal avec un coefficient de frottement f.
On cherche à déterminer expérimentalement le coefficient de frottement
f.
En considérant 2 phases pour le mouvement de M (la deuxième
commence lorsque M′ touche le sol), le but de l'exercice est de
déterminer la distance D parcourue par M avant de s'arrêter et
d'en déduire f, en fonction de m, m′, h et D. O
x
z
h
M′(z)
M(x)
1 . Appliquer le principe fondamental de la dynamique au système {M(m)} puis au système {M′(m′)}.
2 . Intégrer l'équation du mouvement de M (remarquer qu'il existe une relation très simple entre x˙ et z˙ qui découle
de l'inextensibilité du fil) pour déterminer l'instant t1 où M′ touche le sol et la vitesse de M correspondante notée x˙ 1.
JE ME BLOQUE EN QUESTION 2
Bonsoir
Un scan du schéma rendrait l'énoncé plus explicite.
Quelques remarques générales :
Une fois appliqué le PFD à chacune des masses, tu peux faire deux simplifications :
1° : Le fil étant de masse négligeable et la poulie étant idéale, l'ensemble {poulie + fil} conserve la tension du fil.
2° : le fil étant inextensible, à chaque instant, les normes des deux vecteurs accélérations sont égales et les normes des deux vecteurs vitesses sont égales.
Cela devrait te permettre d'avancer et de proposer une solution.
Oui et aussi z"=x" sous réserve que les axes soient orientés convenablement (d'où l'intérêt d'un schéma). On pourrait imaginer des orientations d'axes telles que x'=-z' et x"=-z"...
Il ne s'agit pas d'une "insinuation" mais d'une affirmation . 
Salut les amis , après avoir appliqué le PFD sur les deux systèmes ils me demandent d'intégrer l équation du mouvement de M ( je trouve que x(t)=z(t)+h je ss pas c juste après je me bloque sur la question : déterminer l instant t1 où M' touche le sol et la vitesse de M correspondante . ) tout ça pendant la première phase .
2 phase : intégrer l 'équation du mouvement de M pendant la deuxième phases
- déterminer la distance D en fonction de f puis le coefficient de frottement f en fonction de m , m' , h et D
Mercii les gars de m'indiquer pour chaque réponse
*** message déplacé ***
Bonjour
Cet énoncé a déjà été posté il y a peu de temps.
Postes ce que tu as trouvé et pose si nécessaire des questions précises sur ce que tu ne comprends pas.
Un schéma précis où figurent les vecteurs force aide beaucoup...
*** message déplacé ***
Un peut d'aide tout de même sur la méthode permettant d'obtenir l'accélération pendant la première phase, sachant que les deux masses ont, à chaque instant même vitesse et même accélération.
1° : appliquer la RFD à la masse M' en faisant intervenir M', g et T' la tension du brin de fil vertical ;
2° : appliquer la RFD à la masse M en faisant intervenir, M, g, f et T la tension du brin de fil horizontal.
3° : exprimer l'accélération "a" en remarquant que T = T' puisque le fil est de masse négligeable et que l'énergie de la poulie est négligée. On peut décomposer l'action du plan sur le bloc de masse M en une composante normale N qui compense le poids et une composante tangentielle de frottement F=f.N=f.M.g
*** message déplacé ***



