Inscription / Connexion Nouveau Sujet
Mesure de la distance angulaire
Bonjour,
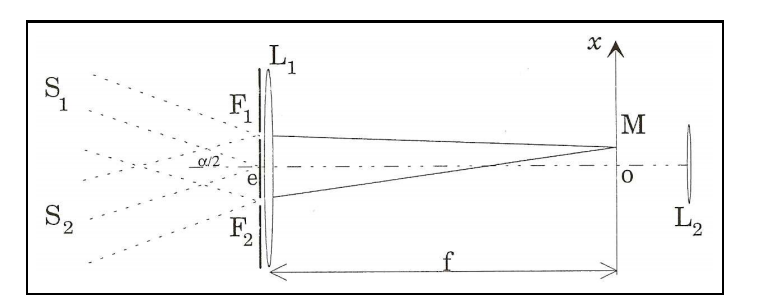
Je suis en train d'essayer de faire un exercice d'optique, mais je bloque à la première question, voici l'énoncé et un schéma en pièce-jointe.
Une lunette astronomique est formée d'un objectif L1 assimilable à une lentille mince de
distance focale f' = l m, et d'un oculaire L2 mis au point sur le plan focal de L1. Elle est
dirigée vers un groupe de deux étoiles très voisines S1 et S2 supposées ponctuelles qui
émettent une lumière monochromatique de longueur d'onde 
et leurs intensités sont respectivement I0 et I'0.
1) On se place d'abord dans le cas d'une unique étoile située sur l'axe de la lunette astronomique. Déterminer la distribution d'intensité au niveau du plan focal image de L1 en un point M (f'>>x).
Pour l'instant, j'ai essayé d'appliquer le principe d'Huygens-Fresnel mais je ne sais pas entre quelles bornes intégrer :
(x) = A0
eik
0e-ikdx.
J'ai pensé à intégrer selon 
mais je ne verrais pas comment faire...
Je n'ai pas encore traité les questions qui suivent, je préfèrerais comprendre la première question avant.
2) Déterminer la distribution d'intensité au niveau du plan focal image de L1 en un
point M(x) en supposant que f >> x.
a) pour la source S1 seule.
b) pour l'ensemble des deux sources (supposées incohérentes entre elles). Dans ce
cas, montrer que l'intensité au point M peut s'écrire:
I(M) = 2(I0 + I'0)¡1+V cos
3) On suppose S1 et S2 de même intensité.
a) Décrire qualitativement la figure d'interférences observée (discuter en fonction
du décalage entre les deux systèmes de franges).
b) Montrer que les franges d'interférences disparaissent pour certaines valeurs de
e. Si la plus petite distance entre F1 et F2 pour laquelle les franges disparaissent
est em = 52 mm, quelle est la distance angulaire entre les étoiles?
Merci d'avance pour l'aide apportée !
Bonjour
Rien n'est dit sur la largeur des deux fentes de Young, je pense que tu te trouves devant un simple problème sur les interférences, sans avoir à faire intervenir la diffraction et le principe de Huygens et Fresnel. Avec une seule étoile, tu te trouves devant l'étude classique des fentes de Young avec deux fentes supposées suffisamment fine pour diffracter avec la même intensité dans toutes les directions du plan de figure. Petite différence par rapport au problème classique où la source est sur l'axe : il faut considérer que la marche de S1 à F2 est plus longue que la marche de S1 à F1 de (e./2) , ce qui induit une différence de phase entre les deux sources F1 et F2. Cela va induire un décalage des franges observées dans le plan focal de la lentille L1 sans modifier l'interfrange. Lorsque S2 est seule, tu vas obtenir un système de franges ayant même interfrange que le précédent mais présentant un décalage.
En présence des deux sources incohérentes mais de même longueur d'onde, les deux systèmes de franges vont se superposer : les intensités lumineuses vont s'ajouter. Si une frange brillante créé par S1 correspond une frange sombre créé par S2, les franges sont invisibles. Elles présentent au contraire un maximum de contraste si les franges brillantes créées par les deux sources coïncident....
Ahh, je n'ai pas encore étudié les fentes d'Young en cours 
.
Je vais essayer de me documenter dessus ou bien j'attendrai que l'on traite ce point en cours.
Tu aurais traité le principe de Huygens et Fresnel et la diffraction sans étudier d'abord les cas simples d'interférences ? Dur, Dur, ton professeur ! 
Annuler
connectez vous