Inscription / Connexion Nouveau Sujet
mesure d'impédances complexes partie 3
Bonjour à tous,
voici la 3ème partie d'un exercice qui me pose problème.
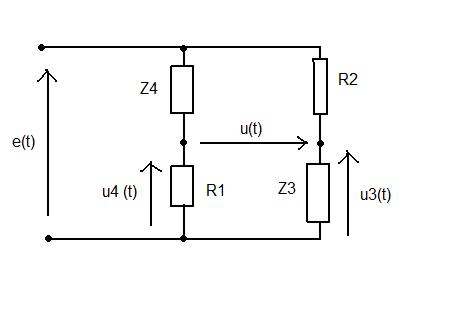
On considère le pont d'impédances suivant : où e(t) est un générateur sinusoïdal de fréquence f = 100Hz et de valeur efficace 5V . R1 et R2 sont deux résistances de 1k
. Z3 est constituée de la bobine à étudier (c'est une bobine réelle donc avec une résistance et une bobine placées en série). Z4 est constituée d'une résistance R en parallèle avec un condensateur C.
1. Exprimer u4 en fonction de e, R1 et Z4.
2. Exprimer u3 en fonction de e, R2 et Z3.
3. En déduire u en fonction de e, R2, R1, Z4 et Z3.
4. En déduire également la condition d'équilibre du pont, c'est à dire la condition
pour que U = 0.
5. Montrer alors que, à l'équilibre du pont : RS = (R1.R2) / R
et que : LS = R1.R2.C
J'avoue ne même pas être capable de faire au moins la question 1, j'ai essayé d'utiliser la loi des mailles et je n'y arrive pas. Je pense qu'il faut que j'utilise la loi d'ohm en courant alternatif U = Z.I
J'aimerais vraiment que quelqu'un m'aide pour ces questions s'il vous plaît, je vous en serai très reconnaissante. D'avance merci à ceux qui m'aideront.
bonsoir
Merci de ta réponse mais pour être franche ça ne m'aide pas ^^' Je vais regarder sur le net ce que c'est et je reviens vers toi ok ?
Re
Voilà ce que j'ai trouvé grâce à ton conseil : e(t) = i(t).(Z4 + R1) et u4 (t) = i(t).R1 tout ça par la loi d'ohm
ensuite j'ai i = e/(Z4 + R1) = u4 / R1 ce qui me donne u4 = (e.R1)/(Z4 + R1) ça m'a l'air d'être ça, j'ai bon ? ^^
Ensuite pour la question 2 je fais pareil
e = i2 (R2 + Z3) et u3 = Z3.i2 par la loi d'ohm
i2 = e/ (R2 + Z3) = u3/Z3 <=> u3 = (e.Z3)/(R2 + Z3)
Si j'ai bon je retire ce que j'ai dit finalement ta réponse m'aura beaucoup aidée, c'est juste que c'est la première fois que je vois le terme de "pont diviseur de tension".
Je vais poster le reste des réponses que j'ai trouvées et j'escompte que toi ou quelqu'un d'autre me dira si c'est juste.
3. je trouve que u(t) = u3(t) - u4(t) = e.Z3/(R2 + Z3) - e.R1/(Z4 + R1) puis en réduisant au même dénominateur et en simplifiant je trouve que
u = (e.Z3.Z4 - e.R1.R2)/[(R2 + R3)(Z4 + R1)]
4. pour que U = 0 il faut que (e.Z3.Z4 - e.R1.R2)/[(R2 + R3)(Z4 + R1)] = 0 <=> (e.Z3.Z4 - e.R1.R2) = 0
<=> e.Z3.Z4 = e.R1.R2 <=> Z3.Z4 = R1.R2
je crois que c'est juste, j'ai vu une propriété sur internet qui parlait de produit en croix, mais je n'ai pas tout saisi.
5. Là je ne sais pas trop, pour que RS = (R1.R2) / R soit vraie il faut que Z4 = R et que Z3 = RS mais je ne sais même âs d'où ça sort, c'est surement une propriété du circuit. Tu pourrais m'expliquer stp.
et pour la toute dernière formule je ne sais pas :/
Merci par avance de m'aider ^^
Ok, très bien,
donc Z3.Z4 = R1.R2, ce qui donne en remplaçant Z3 et Z4 si
Z3 est constituée de la bobine à étudier (c'est une bobine réelle donc avec une résistance et une bobine placées en série). Z4 est constituée d'une résistance R en parallèle avec un condensateur C
oh j'ai (je crois...)
si je remplace Z3 par LS (pour la bobine) et Z4 par 1/C ça marche car j'ai LS/C = R1.R2 et j'obtiens ma dernière formule. C'est ça ?
Bonsoir à toi,
ok alors Z3 serait égal à LS + RS ? Et Z4 = 1/C + R ?
et Z4.Z3 = (1/C + R).(LS + RS) = (L + RS)/C + RL + R.RS
Je crois que je ne te suis plus ^^ (sauf si j'ai fait une faute)
Remarque : J'ai vu sur le net qu'en régime sinusoïdal RS (donc pour la bobine) était nul, tu crois que je peux m'en servir ici.
Je sais que la solution est toute proche mais je ne la vois pas encore c'est frustrant ^^' en tout cas c'est vraiment aimable de ta part de prendre de ton temps pour moi.
En réduisant au même dénominateur 1/Z4 = (1 + R.j.C.w)/R donc Z4 = R/ (1 + R.j.C.w)
A mon sens il faut virer les imaginaires mais je ne sais pas comment faire pour l'instant...
Re bonjour,
ok alors j'ai fait le produit Z3.Z4 = R1.R2 avec Z3 = R + jLw et Z4 = R/ (1 + R.j.C.w)
je trouve en réduisant au même dénominateur et en simplifiant L = [R1.R2 * (1 + j.R.C.w)-R²] / j.R.w
j'ai multiplié par j au numérateur et au dénominateur et j'obtiens L = [-R.R1.R2.C.w + j(R1.R2-R²)] / (-R.w)
par simplification j'ai L = R1.R2.C - j[(R2.R2 - R²)/R.w] Miracle ! je vois enfin mon terme apparaître 
mais j'ai toujours des imaginaires --'
Dis moi que le terme en imaginaires est nul stp xD
Une petite formule magique pour m'aider ? ^^
Au fait, je ne sais pas si c'est considéré comme du multipost (si c'est le cas je ne le ferai plus) mais tu pourrais jeter un oeil à un autre sujet que j'ai mis en ligne nommé "mesure d'impédances complexes 1 bis" j'ai répondu à toutes les questions mais je ne suis pas sûre de la question 4.
Un membre m'a fait comprendre que je n'avais pas assez de difficultés à son sens pour être digne d'aide, alors que j'en ai vraiment besoin :/
Ce serait vraiment sympa de ta part si tu pouvais vérifier.
Annuler
connectez vous