Bonjour à tous, je bloque sur la dernière question d'un exercice.

On a un système :



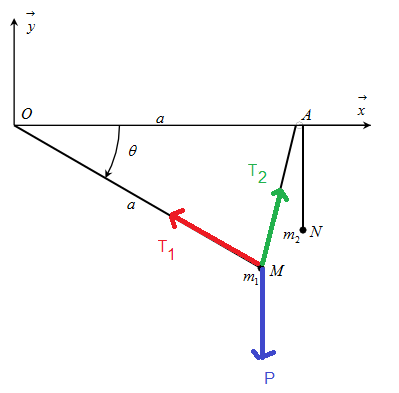
En A on a une poulie négligeable et le système est à l'équilibre.

1) Calculer le poids de m₁ dans (0,x,y,z).

P = -mg y


2) Calculer la tension du fil T₂.

T₂ = m₂g(sin(θ/2) x + cos(θ/2) y)


3) Déduire T₁ en appliquant le PFD.

T₁ = -m₂g*sin(θ/2) x  +  g(m₁-m₂*cos(θ/2))


4) Calculer le moment en O de P.

M_O(P) = -a*m₁g*cos(θ) z


5) Calculer le moment en O de T₁.

M_O(T₁) = a*m₁g*cos(θ) - a*m₂g*cos(θ/2) z


6) Calculer le moment en O de T₂.

M_O(T₂) = a*m₂g*cos(θ/2) z


7) Appliquer le théorème du moment dynamique au point O à la masse m₁. En déduire une condition entre m₁, m₂ et θ pour qu'une positon d'équilibre existe.

dL_O/dt = M_O(F_m1) = 0

La seul chose que je trouve c'est :

v_x = sin(θ)/cos(θ) v_y

Merci d'avance.