Bonjour,

Merci beaucoup pour votre aide,

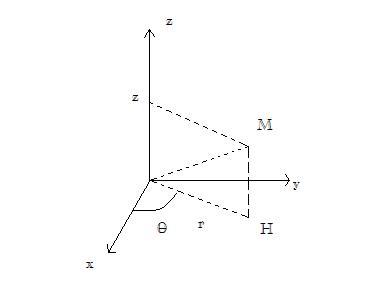
Un point M est repéré par ses coordonnées cylindriques (r,,z) centrées sur le noyau galactique C (voir figure ci dessous).

L'axe z est aligné avec l'axe de symétrie de la galaxie et le potentiel asymétrique U est fonction des seules coordonnées r et z, soit U=U(r,z); en outre, la fonction U(r,z) est symétrique par rapport au plan équatorial z=0 et on a donc U(r,z)=U(r,-z)

1) Justifier brièvement que (u/z)_r(r,0)=0

2)a)Ecrire la relation fondamentale de la dynamique et en déduire 3 équations du mouvement (utilisant les coordonnées cylindriques r,,z et le potentiel U ou ses dérivées par rapport à r,,z)

b)Montrer que la composante du moment cinétique de la particule sur l'axe Oz est conservée au cours du mouvement, on notera Lo cette constante.

c)En déduire que l'étude générale du mouvement du point M peut alors être ramené à un problème à deux inconnuesr et z régi par les équations

r"=-(Ueff/r)z

et

z"=-(Ueff/z)r

dans le plan méridien (CMH).

Merci pour vos réponses!