Inscription / Connexion Nouveau Sujet
Mécanique: ressort
Bonjour,
J'aurai besoin d'aide concernant une question d'un de mes TP.
Il s'agit de déterminer l'équation différentielle du système suivant.
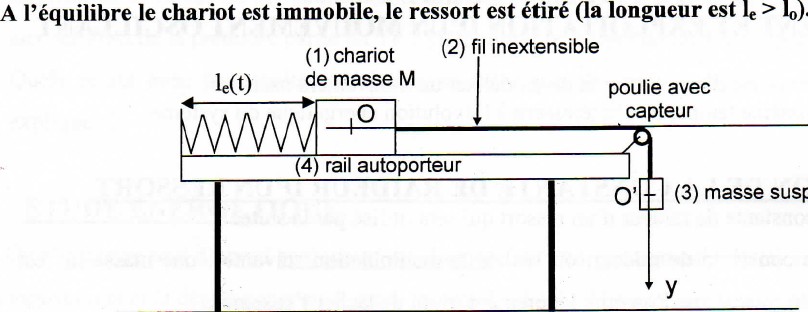
On a un chariot de masse M et une masse de masse m.
On a démontré au préalable que la force de Tension du câble T sur le chariot est égale à T', celle exercée sur la masse m.
La force de frottements fluide est notée: hx.
La force de frottements solide est notée: 
F
On sait aussi que x(t)=y(t).
De ce fait, j'ai utilisé la loi de Newton 
Fext=ma au niveau du chariot selon .
Puis, sur la masse, selon
.
J'ai donc par la suite exprimé T et T':
T=Mx.. + hx. +kx F (lire Mx point point et hx point)
T'=mg-my..
J'ai égalisé et j'obtiens:
(M+m)x.. + hx. + kx = F + mg
Or selon le sujet, il nous est dit que l'équation est égale uniquement à F, qu'il n'y a pas de mg.
Comment est ce que je pourrai enlever le "mg", à moins de le remplacer par sa valeur numérique ce qui me semble peu probable.
Merci de vos réponses.
PS: Vous trouverez le système ici *** lien vers ton ordinateur effacé ***
Edit Coll
bonsoir,
g doit intervenir a priori dans la solution puis que le poids de la masse m travaille
tu as dû rater un épisode, un changement de variable par ex.
Cela dépend où l'origine des x a été prise. (Cela n'est pas précisé dans ton énoncé)
Si c'est la position du centre d'inertie de M quand le système est au repos comme si il n'y avait pas de frottement sec, alors ton x serait à remplacer par X + mg/k (pour tenir compte de l'allongement du ressort de constante k sous l'effet du poids mg)
Dans ce cas, on aurait :
dx/dt = dX/dt et d²x/dt² = d²X/dt² et l'équation deviendrait :
(M+m).d²x/dt² + h.dx/dt + k.x = mg +/- F
(M+m).d²X/dt² + h.dX/dt + k.(X + mg/k) = mg +/- F
(M+m).d²X/dt² + h.dX/dt + k.X = +/- F
(Il faut évidemment préciser quand prendre le + ou le - du +/- F ...)
-----
Sauf distraction. 
Annuler
connectez vous