Bonsoir,

Si j'ai bien compris on a quelchose de ce goût là :

Bonsoir, oui c'est exactement ça

bonsoir,

sujet original.

je vois 3 situations possibles selon l'angle que fait la tangente de la parabole (et donc Vo) avec (OA)

le 1er cas a été représenté ci-dessus: angle (OA,Vo) < 90°

mais il y a d'autres configurations possibles

pardon:
je vois 3 situations possibles selon l'angle que fait la tangente de la parabole en A

J'ai déduis ce cas parce que j'ai presque résolu un exo traitant du cas schématisé et je me demande donc si il n'y aurait aurait pas d'autre détails omis ici.

Quoi qu'il en soit, je vois rapidement 2 cas où le projectile pourrait repasser en O mais le 3ieme je ne comprend pas.

Pour ce qui ait de la Q3, voici mes pistes (je ne sais pas si l'hypothèse de départ est correcte) :
Le passage en O après rebond implique que les trajectoires av et ap rebond soient identiques et donc que le vecteur vitesse en A soit colinéaire à la normale au plan incliné.
J'ai ensuite déterminé l'équation de la trajectoire : .
En dérivant cette expression on obtient la tangente de l'angle de la trajectoire et il faudrait la valeur de cette tangente en ensuite on simplifie et on égalise à (c'est la tangente de l'angle à la trajectoire en A. Mais c'est là que ça se gâte : je n'aboutis pas au bon résultat donc soit mon hypothèse de départ est fausse soit j'ai mal calculé.

En espérant avoir aidé et avoir un retour sur ma méthode.

oops j'ai oublié de fermer la parenthèse après le tan alpha (dans Xa).

Peut-tu développer un peu krinn ?? Je pense je ne traite que d'un cas parmi les trois ici. Je ne comprends pas les 2 autres...

1) la trajectoire de la balle est une branche de parabole (tir parabolique)
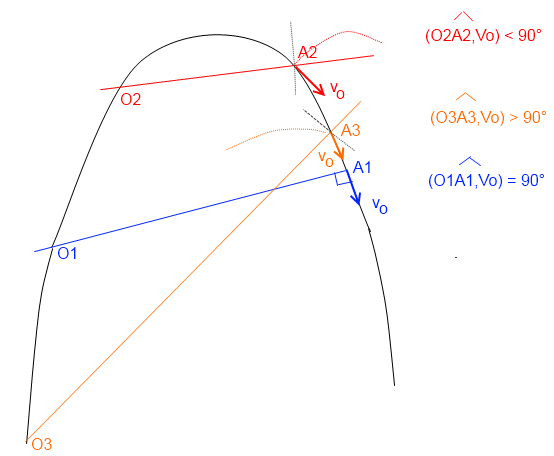
la figure qui suit montre les 3 situations possibles (que l'on peut toujours construire avec une telle parabole) :
j'ai représenté à chaque fois la pente (OA), la normale à (OA) en noir, et Vo, vitesse juste avant le rebond en A.
le cas 3 (en orange) correspond au rebond en arrière.

2) comme l'a bien vu oola, seul le cas 1 (en bleu) peut permettre à la balle de revenir en O
il faut que v1 soit normale à (OA) et |v1|=|vo| pour que la trajectoire soit la même au retour


(je sais, ma parabole est horrible

tu y étais presque, oola.

ta solution consiste à écrire que la tangente à la parabole en A est normale à (OA)
si y(x) est l'éq. de la trajectoire
on a donc: y'(x_A) = pente de la tangente à la parabole en A = - tg( pi/2 - ) = -1/tg
attention! la pente est négative!

en notant = +
on trouve après calcul de xA puis de y'(x_A) :

xA = 2Vo²cos²(tg-tg)/g

y'(x_A) = -2(tg-tg) + tg = -1/tg

c'est la seonde relation qui donne

-2(tg-tg) + tg = -1/tg
<=> 2(tg-tg) = 1/tg + tg = (1 + tg tg ) / tg

<=> 2 tg = (1 + tg tg ) / (tg-tg)

et c'est là que ça bloque quand on a oublié ses formules de trigo, ce qui est mon cas

tg(a-b) = (tga -tgb) / (1 + tga.tgb)

donc (1 + tga.tgb) / (tga -tgb) = 1/tg(a-b)

et en remplçant qu-dessus ça s'arrange et tu retrouves la relation cherchée

NB: il ya peut-être une solution plus simple.

Effectivement je n'ai pas fait attention à la pente !!

Mais je ne comprends pas comment tu passes de 2(tg-tg)= ....
à 2tg = (1+tgtg)...

tu passe tg à gauche
et (tg-tg) à droite

ah oui tout bêtement ^^

Houra j'ai enfin conclut. Et dire que ne n'était qu'à cause d'une bête erreur !!

c'était loin d'être évident.
est-ce que la formule donnant Beta était indiquée dans l'énoncé?

pour moi oui mais je ne l'ai pas regardée et je l'ai cachée (je cache d'ailleurs toutes les réponse car notre prof les met tjrs!)

dans certains cas on donne la réponse pour que les élèves ne soient pas bloqués par une question difficile.
(c'est d'ailleurs un indice que la question n'est pas évidente et qu'il ne faut pas perdre trop de temps dessus!)

Ici c'est le cas, à mon avis