Personne n'a d'idée ?
Je peux reformuler mon problème si vous voulez.

Merci

Bonjour Johnz,

moi si, j'ai des idees pour resoudre ton probleme : ton post est sur mon bureau depuis mardi soir, mais je n'ai pas encore eu le temps de taper la reponse. Je vais essayer de faire ca ce soir (au moins une version succincte) et si oui, tu recevras un post ce soir meme ou demain dans le courant de l'am. Ne desespere pas, ce n'est pas difficile. Le pb est qu'il y a des formules a taper et que c'est ca qui prend du temps.

A tres bientot,  prbebo.

Bonjour Prbebo,
merci,j'apprécie beaucoup votre geste, c'est vraiment gentil.

Ne vous embêter pas trop pour taper les formules, c'est vrai que c'est long. Si vous voulez vous pouvez me dire les opérations à faire au lieu de les taper, c'est surtout vos explications, votre raisonnement qui m'interesse car je pense que j'ai fais de grosse erreurs (notamment pour Fic et Fie)
Serait il possible que vous m'en parliez dès ce soir ?

Merci encore.

Oui, car je viens juste de terminer la figure (cad la tienne + les forces appliquees a la masse m. A ce soir,  BB.

D'accord, merci d'avance.

Bonsoir,
j'ai continué de chercher de mon côté et je pense avoir déterminer des erreurs (j'ai cherché à appliquer les formules "toute faite" pour Fic et Fie) alors je suis revenu à la formule de départ.

Fie
a:accélération
d: dérivée
a(o') par rapport à R est nul car o' est confondu avec o.
Vitesse angulaire constante donc sa dérivée est nule.
Ceci simplifie bien la formule est je trouve au final,



Fic


Merci

Pardon pour le double post.
J'ai oublié de préciser que je remplacer w par Vo/Ro comme le demande la consigne mais par contre comment "faire disparaître" x'1.
J'ai considérer x'1 comme la composante relative à O'M et donc sa dérivée correspond à V(M)R'
Merci encore

Bonsoir Johnz,

me revoici enfin. Je vais repondre globalement a ton probleme, sans respecter l'ordre des questions. D'abord parce que je te sens suffisamment mature pour remettre tout dans l'ordre, ensuite parce que je ne suis pas trop d'accord avec l'ordre dans lequel ces questions sont posees (par exemple, la question 4 aurait du arriver plus tot, et la fin de la question 6 n'a aucun interet puisque sa reponse est contenue dans les deux premieres lignes de l'enonce).

Le cerceau est parcouru avec une vitesse V₀ constante (je parle de la norme du vecteur vitesse), donc le mouvement de M est circulaire et uniforme. La vitesse angulaire est donc bien = V₀ / R, et comme les axes x1 et x'1 sont confondus a l'instant initial, la loi horaire donnant l'angle entre ces deux axes est (t) = t. C'est ce que tu as trouve.

Puisque dans le mouvement de M est circulaire et uniforme sue un cercle de rayon R parcouru a la vitesse angulaire , et que le mouvement du repere (R') par rapport a (R) est une rotation avec cette meme vitesse angulaire, c'est que dans (R') M semble immobile. Ceci implique que l'on peut ecrire dans (R') somme des forces = 0, mais attention : (R') est en rotation donc n'est pas un referentiel galileen. Donc les forces a comptabiliser sont les forces reelles (poids + reaction de l'anneau), plus les deux forces "fictives" ou "inertielles". Ces deux foeces sont : la force inertielle d'entrainement, qui s'ecrit Fie = - m.ae, et la force ce Coriolis Fic = - m._ac. (NB je mets en gras les quantites vectorielles, car je ne sais pas encore bien les faire avec l'editeur d'equations du forum... ca viendra !).
Parlons tout de suite de la force de Coriolis : tu sais j'en suis sur que son expression depend de la vitesse angulaire et de la vitesse relative v_R par la relation a_C = 2.v_R. Or dans cet exercice il n'y a pas de mouvement relatif. Donc v_R est nulle, et l'acceleration de Coriolis aussi.
en revanche l'acceleration d'entrainement, elle, n'est pas nulle : elle correspond a l'acceleration d'un point qui tourne sur un cercle de rayon R a la vitesse angulaire , soit a_e = - ²R.ex'₁ (sng - car elle est dirigee de M vers O).

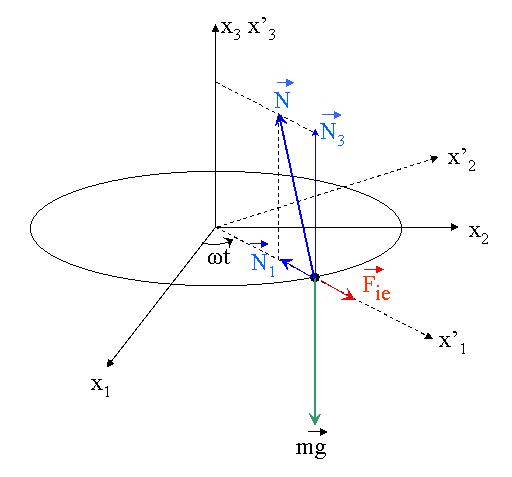
Si on recapitule : la force fictive d'entrainement vaut F_ie = m.²R.ex'₁, representee en rouge sur mon schema, et la force fictive de Coriolis est nulle.

Parlons maintenant de la reaction N de l'anneau sur la masse : elle a a priori trois composantes, N1, N2 et N3. mais on peut savoir tout de suite que N2 est nulle. Pourquoi ? parce que le mouvement se fait sans frottement. Donc la reaction N n'a pas de composante sur la tangente a la trajectoire, tangente dont la direction est donnee par l'axe x'2 (s'il y avait frottement, cette composante serait portee par x'2 et dirigee dans le sens negatif, car s'opposant au mouvement de M).

Appliquons maintenant le PFD dans le referentiel (R') : puisque la vitesse relative y est constamment nulle, c'est que l'acceleration relative l'est aussi, et donc le PFD donne somme des forces = 0, a condition d'y incorporer les forces reelles (poids et N) et fictive (entrainement).
Bon, pa la peine de faire un dessin : le PFD, projete sur l'axe x'1, donne N1 = Fie = m²R ; sur x'2 il ne donne rien, et sur x'3 on obtient N3 = mg.

Les equations parametriques du mouvement de M dans (R) ne sont pas trop dures a trouver :
x(t) = R.cos(t), x2(t) = R.sin(t), x3(t) = 0.

J'espere avoir repondu a toutes tes questions.

A bientot, BB.

Bonsoir Prbebo.

Un énorme Merci pour votre réponse précise et explicite. Vous avez dû passé beaucoup temps à rédiger et à réaliser le schéma afin que je comprenne. Donc je tiens, tout d'abord, à vous remercier.

J'ai tout de même quelques questions.
Je pense avoir compris l'explication avec la vitesse angulaire et le fait que M semble immobile. Par contre, je bloque sur la force de Coriolis, je ne comprends pas pourquoi V(M)_r' est nulle. (est ce parce qu'on le considère immobile dans R' ? Parce que sinon, il suffirait que je cherche la vitesse de M dans R et que j'utilise la formule pour changer de référentiel et trouver la vitesse de M dans R')

Pour Fie, je suis entièrement d'accord et pour le reste aussi. (je vais vérifier si j'obtiens le même résultat pour les équations paramétriques)

Merci d'avance.

Bonsoir,
j'ai eu une "illumination" pour mon problème avec Coriolis.(j'ai cherché à calculer la vitesse et donc tout d'abord le vecteur position).

O'M= R ex'1

Or R est le rayon qui constant donc di je dérive pour déterminer V(M)_r', je trouverais une vitesse nulle et donc une force Coriolis nulle.

Est ce correct ?
Merci

Bonjour Johnz,

oui c'est correct mais n'oublie pas que ce raisonnement n'est vrai que si on se place dans le referentiel relatif (R'), le seul qui permette d'"oublier" les derivees des vecteurs unitaires e'x1, e'x2 et e'x3. Autrement il faut les faire intervenir dans la derivee de OM, ce qui conduit aux expressions de la vitesse et de l'acceleration absolues.

Il y a un raisonnement simple pour trouver sans calcul que V_R est nulle : imagine un observateur immobile dans (R'), par exemple ligote sur l'axe OX'3 et, pour simplifier, oriente pour regarder dans la direction de OX'1 ; cet observateur a donc constamment le point M devant lui. Si la distance OM varie, il verra M s'eloigner ou se rapprocher de lui tjs dans la direction de OX'1 et en deduira que V_R est portee par cet axe. Dans ton exercice OM = R donc ne varie pas, et pour l'observateur assujetti a (R') M est immobile. La vitesse relative VR est donc bien nulle.

Pour l'acceleration de Coriolis, pas  de pb : son expression vectorielle montre qu'elle est directement reliee a V_R, donc nulle elle aussi dans ce pb.

En conclusion :
V_R = 0, V_E = V_A = Rex'2 ;
a_R = a_C = 0, a_E = a_A = -²R.ex'1.

Pour projeter les vecteurs non nuls dans le referentiel absolu (R), tu peux utiliser les relations de passage :
ex'1 = cos.ex1 + sin.ex2,
ex'2 = -sin.ex1 + cos.ex2, avec = t.

Ce n'est pas la figure qui m'a pris du temps, mais c'est le texte !

A une prochaine fois peut-etre.  BB.

Bonjour,
je vous remercie de vos explications, cela m'a beaucoup aidé et je pense avoir tout compris.
Alors Un GRAND MERCi à vous.

Cordialement,

Johnz

Bonjour Johnz,

eh bien ca fait plaisir que mes explications ont servi a quelque chose, et aussi de voir qu'il y a des eleves qui prennent le temps de remercier apres avoir ete depannes. Je suis sur que tous les correcteurs du forum seront de mon avis !

Bonne  chance pour les examens s'ils ne sont pas encore passes, et a bientot pour d'autres interventions.  B.B.

C'est tout à fait normal.
Merci et bonne continuation à vous.

-Johnz

Bonjour !
Je me permet de remonter ce topic dans la mesure où j'ai trouvé qu'il y avait d'autres questions liées à cet exercice et qui me posent certains problèmes (merci à la modération mais si cela est dérangeant, je peux créer un nouveau topic).

Voici la suite des questions:

Je n'ai pas eu le courage de lire tout le topic et donc aux risques de redites ...

Problème initial :

1)
wo = Vo/Ro
theta(t) = wo.t

2)
Poids de m
Force centrifuge.
réaction du cerceau.

3)
P = -m.g.vect(u'3)
Fc = mVo/Ro . vect(u'1)

4)
m est immobile

5)
La somme vectorielle des 3 forces du point 2 est nulle et donc :

N1 = -mVo/Ro . vect(u'1)
N2 = 0
N3 = m.g.vect(u'3)

6)
x1(t) = Ro.cos(wo.t)
x2(t) = Ro.sin(wo.t)
x3(t) = 0

Mouvement circulaire uniforme.
-----
Suite (message précédent):

1)
Em = mgz + (1/2).m.Vo² (sans frottement je présume ??)

2)
Delta Em = 0 puisque l'altitude z de la masse reste constante et que la vitesse instantanée de la masse est constante (Vo) (sans frottement je présume).

3) Ec = (1/2).m.V²

4) |Ff| = µ.m.v/Ro
dv/dt = - µ.v/Ro

dv/dt + µ.v/Ro = 0
(Avec V(0) = Vo)

Equation qui résolue donne = v(t) = Vo.e^((-µ/Ro).t)
-----

Sauf distraction. Vérifie.

Bonjour,
merci d'avoir répondu, j'ai surtout des questions sur la deuxième partie.