Inscription / Connexion Nouveau Sujet
Mécanique: Pendule Simple
Bonsoir,
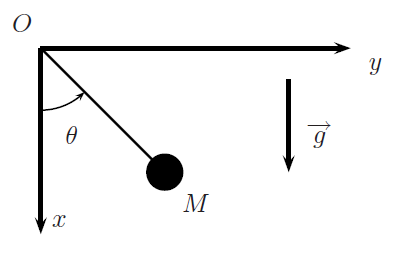
Je bloque sur une partie du programme de mécanique, j'ai du mal avec tous les exercices qui sont similaires à celui du pendule simple. Je voulais donc vous posez une question, et demander non pas seulement la réponse mais une méthode pour la trouver. Je m'explique, par exemple en partant du schema ci dessous.
Il faut faire le RFD pour trouver l'équation, ici P + T= m.a
J'arrive tant bien que mal à projeter les forces , mais dans la réponse il semble qu'on projette aussi m.a (?) tel que:
m.a = -ml
'2er
ml''e
J'aimerais savoir comment arriver à ce résultat.
Merci d'avance.
bonjour,
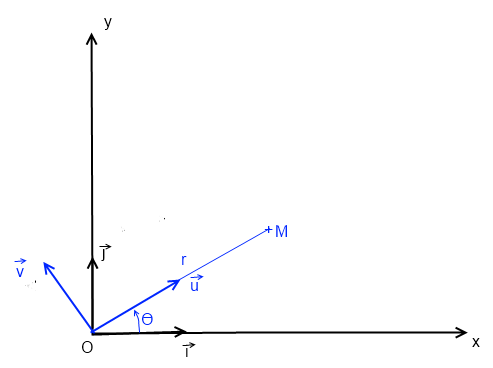
c'est un résultat qui s'obtient par dérivation vectorielle de OM dans une base donnée
(vecteurs en gras)
ici, en corrdonnée polaires ( base (
,
):
OM = r
V(M) = d/dt(r) = dr/dt + r d /dt = dr/dt + rO'
a(M) = d/dt V(M) = ... = (r" - rO'2) + (rO" + 2r'O')
si r=cste ça se simplifie (r'=r"=0)
Ah tout s'explique ! Merci beaucoup !
J'ai une autre question à propos de la résolution de l'équation différentielle.
En continuant j'ai donc:
'' + (g/l) = 0
Je dois donc faire
r² + 0r + (g/l)
= -(4g/l)
Donc solution de la forme:
(t) = e
(Acos( 
t) + Bsin(t))
r1= i
(g/l)
donc j'obtiens
(t) = Acos((g/l)*t ) + Bsin((g/l)*t)
Pourtant la réponse attendue est (t) = Acos((g/l).t + C)
Je voulais savoir comment on en arrivait là.
Il est toujours possible de transformer (A.cos(racine(g/L).t) + B.sin(racine(g/L).t)) en D.cos(racine(g/L).t + Phi)
-----
Annuler
connectez vous