Inscription / Connexion Nouveau Sujet
Mécanique dynamique
Bonsoir, je suis en première année de licence informatique et il y a dans mes modules de la mécanique que je ne maîtrise absolument pas puisque j'ai fait math et nsi en terminale. J'ai bcp de mal à comprendre. Quelqu'un pourrait-il m'aider sur ce sujet ?
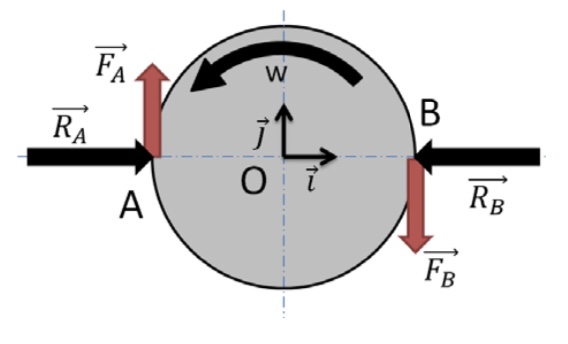
Un disque de rayon R tourne autour d'un axe OZ avec une vitesse angulaire constante w. 2 forces radiales Ra et Rb sont alors appliquées en A et en B. Ces forces génèrent des forces de frottement Fa et Fb dont le sens est opposé au sens de rotation du disque. Le moment d'inertie d'un disque de centre O, de rayon R et de masse m étant égal à Ioz =mR2(carré)/2, au bout de combien de temps le disque va-t-il s'arrêter si : w = 10rad/s
R =10cm m=1kg Ra =Rb=100N
Fa =Fb=10N
Je vous remercie pour toute aide que vous m'apporterez 🙏
Bonjour
Connais-tu le théorème du moment dynamique (aussi appelé théorème du moment cinétique) qui fournit le produit du moment d'inertie par l'accélération angulaire en fonction des moments des forces extérieures ?
Il s'agit ici d'une application directe de ce théorème puisqu'il faut commencer ici par calculer l'accélération angulaire (valeur négative ici si le sens positif de rotation choisi est le sens du mouvement).
Bonjour, merci bcp de prendre de votre temps.
Oui je connais ce théorème mais je ne sais pas l'appliquer ☹️
Il faut l'appliquer ici au disque en prenant comme axe l'axe de rotation (O,z) perpendiculaire au plan de figure. As-tu appris à déterminer le moment d'une force par rapport à un axe ?
Oui. Le résultat est assez simpleici. Attention aux signes : le moment par rapport à l'axe vaut -F.d si la force tend à faire tourner le solide dans le sens négatif.
Somme des moments qui est égale au produit du moment d'inertie par la dérivée seconde de l'angle de rotation. Mais comment calculer cette dérivée seconde ?
Erreur pour les moments de RA et RB. Les lignes d'action de ces deux forces rencontrent l'axe de rotation. Le bras de levier "d" est donc nul dans les deux cas. La somme des moments par rapport à l'axe de rotation vaut donc MOz=-2N.m.
En notant 
" l'accélération angulaire, le théorème du moment cinétique conduit à :
IOz."=MOz
Les équations du mouvement sont analogues à celles obtenues pour le mouvement rectiligne uniformément varié. Il suffit de remplacer l'accélération"a" par l'accélération angulaire ", la vitesse "v" par la vitesse angulaire '=
et l'abscisse "x" par l'abscisse angulaire (angle de rotation) .
En mouvement rectiligne uniformément varié, tu as (programme de terminale) :
v=a.t+vo
Ici, pour un mouvement de rotation uniformément varié :
'=".t+'o
En prenant comme instant initial le début du freinage : 'o==10rad/s
Tu as déterminé l'accélération angulaire précédemment...
C'est bien là mon problème, je n'ai pas fait la spé physique en terminale ☹️ Je dois rattraper le programme toute seule et c'est pas facile!
Merci à vous en tout cas….
D'après vos données, theta0 =10, theta'´= -40 et on considère thêta' =0 (à l'arrêt)
Je trouve t = 0,025s
Pas sûre du tout 😵💫
Des erreurs qui semblent se compenser. Selon moi, l'accélération angulaire vaut -400rad/s2 (ne pas oublier l'unité). Sachant que la vitesse initiale vaut 10rad/s, la durée de freinage vaut 2,5.10-2s.
Annuler
connectez vous