Inscription / Connexion Nouveau Sujet
Mécanique du solide, train d'engrenages
Bonjour, voici un énoncé d'exercice. Je me débrouille très bien en mécanique, mais dans ce cas, j'ai du mal... j'espère que vous saurez m'aider :
"3 roues dont les centre sont aligné sur un arbre (cf schéma), sont en contact 2à2, sans glissement. L'arbre tourne autour de CI de la roue S1 de rayon R1 avec une rotation instantanée . S1 est fixe. Les autres roues peuvent tourner autour de leurs centres avec des vitesses angulaires
2 et 3. On dèfini le système d'axe {
;
;
} lié à l'arbre (et donc à S1). Soit A le point de contact entre S1 et S2, et B le point de contact entre S et S3.
Hypothèse : toutes les vitesses de glissement entre les roues, sontn nulles.
Question : calculer 2 et 3 en fonction de 
, et des rayons."
Entre S1 et S2, c'est assez simple. Je defini RT, la base tournante {;;}.
Donc
La vitesse de A, sur S1 par rapport à RT est nulle.
Ainsi :
Mais là je bloque.. le premier terme serait alors nul ! Mais à la fin, on doit trouver :
.
Pouvez vous m'expliquer? Je n'arrive pas à poser les bonnes bases, je sais pas.. dites moi.
Merci d'avance !
bonsoir,
si j'ai bien compris ton énoncé,
pourquoi n'exprimes-tu pas les vitesses dans le repère fixe R1 (lié à S1 qui est fixe) (cf dessin)
meme si tu as le droit d'utiliser RT pour calculer la vitesse de glissement, ça complique les choses à mon avis
et on risque de se tromper:
La vitesse de A, sur S1 par rapport à RT est nulle.
non, A
S1 n'est pas fixe dans RT
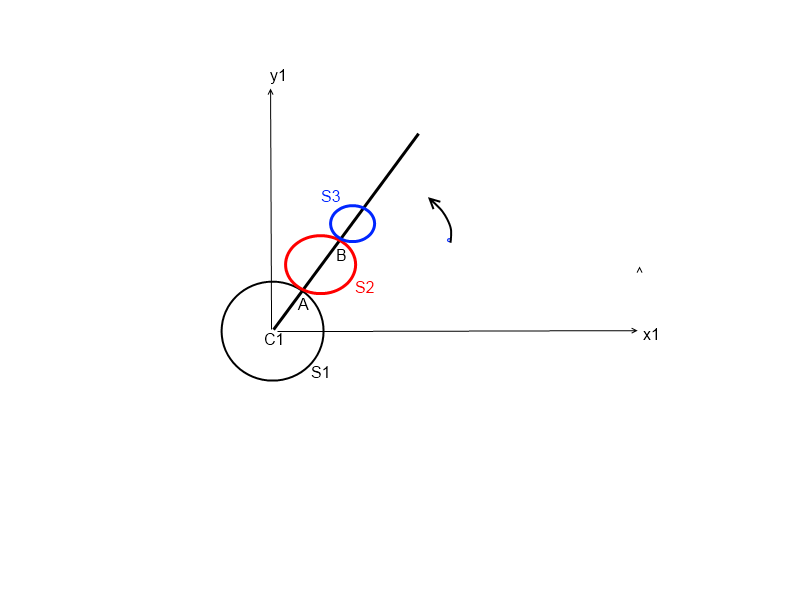
Oui, le dessin, c'est bien ca ! Et le ref dont tu parles, lié à S1, c'est mon RT qui tourne avec l'arbre.
Et V de AS1/RT=V de CIS1/RT+S1/R[sub]T[/sub]=V de CIS1/RT=O
car S1 tourne pas par rapport à RT
L'arbre tourne autour de CI de la roue S1 de rayon R1 avec une rotation instantanée . S1 est fixe.
S1 étant FIXE et RT lié à l'arbre, RT ne peut pas être lié à S1
R1 et RT sont bien différents
Moi je comprends fixe = S1 est lié à l'arbre, il n'a pas de rotation.
Mais selon votre version, que trouvez vous comme relation entre et ainsi que les rayon R1 et R2 ? Si vous trouvez la meme chose ce que j'ai marqué plus haut, pouvez vous m'expmiquer ?
Mon problème, c'est je ne trouve pas ps le bon résultat.. alors que j'ai fais les calculs dans 2ref différents. (Les deux résultats étaient identiques : =II
soit:
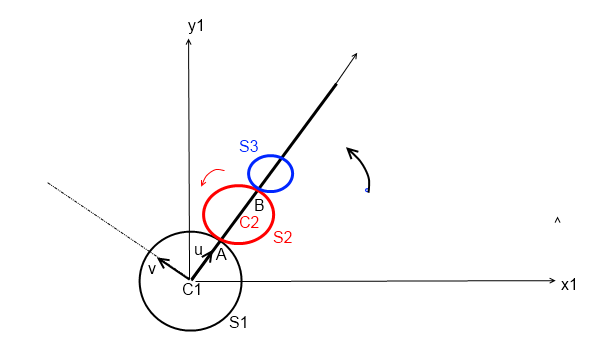
RT(,
) le repère lié à l'arbre
R1(C1,x1,y1) le repère fixe
A1: point A appartenant à S1
A2: point A appartenant à S2
l'arbre n'entraine que S2 et S3, pas S1
Vg(S2/S1) = V(A2)/R1 - V(A1)/R1 = V(A2)/R1 - 0 = V(A2)/R1
V(A2)/R1 = V(C2)/R1 - w2 R2
= (R1+R2) - w2 R2
donc s'il n'y pas pas glissement de S2 / S1 on a:
V(A2)/R1 = 0 ce qui donne la relation cherchée
sauf erreur
Mon problème est toujours là.. je ne comprends pas pourquoi la vitesse de A1 par rapport à R1 est nulle. A se déplace sur le cercle, non ?
A1 est le point de S1 coïncidant avec A à un instant donné, mais il est lié à S1 donc ici il est fixe puisque S1 est fixe.
A, A1 et A2 n'ont pas la meme trajectoire, ils ne coïncident qu'à un instant donné, ensuite ils "vivent leur vie" 
A se déplace sur le cercle (mais n'est pas lié aux solides) tandis que A1 est lié à S1 et A2 est lié à S2
et ce sont les vitesses de A1 et A2 qui importent pour calculer Vg
Aaah d'accord ! Je vous remercie, je viens de comprendre la subtilité tu problèmes ! A1 N'est pas le pt de contact, mais c'est juste un point coïncident à un certain moment ! ? C'est bien ça ?
oui, c'est pour cela qu'on note en général AS1 ou encore A1 et non pas simplement A pour éviter les confusions lors du calcul des vitesses
Annuler
connectez vous