Voici l'énoncé de mon exercice  avec quelques éléments de réponses. Pouvez-vous m'apporter quelques précisons pour le calcul du glissement demandé et des indications pour que je puisse continuer à partir du 3e), je vous remercie par avance.

On s'intéresse à une roue, de centre de gravité C, ayant les caractéristiques suivantes : masse M, rayon a, moment d'inertie par rapport à son axe de symétrie : ²

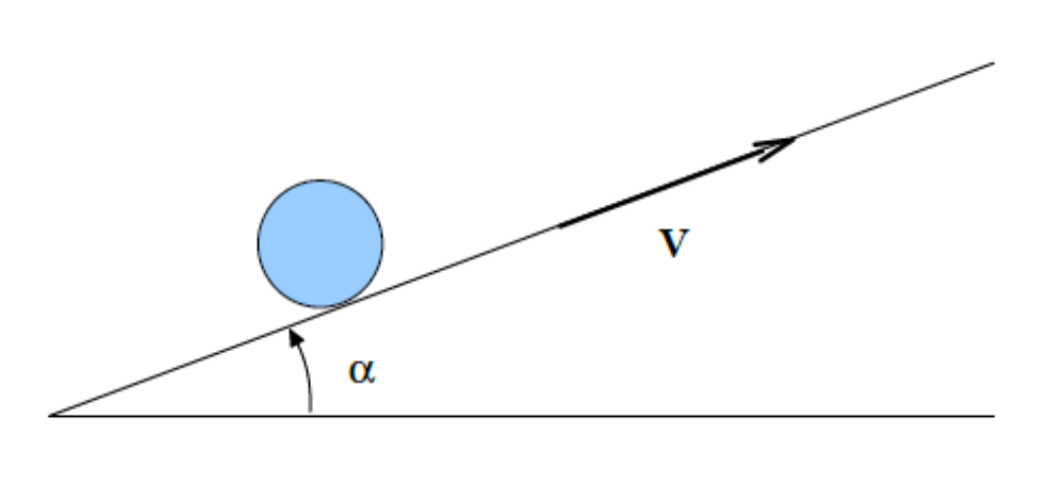
Le tapis roulant est en mouvement avec le vecteur vitesse \vec{V} pour sa partie supérieure depuis un temps long. La roue est alors posée sans vitesse de son centre d'inertie et sans vecteur rotation sur le tapis roulant (supposé en mouvement avec le vecteur vitesse \vec{V} ) à l'instant t  0 que l'on prendra comme origine des temps. On supposera que la norme de \vec{V} est constante et égale à V avec V  0 . Ce tapis roulant fait un angle alpha  avec l'horizontale.

On supposera le contact entre la roue et son support horizontal ponctuel. Le coefficient de frottement de la roue sur le sol sera supposé constant et noté f qu'il soit statique ou cinétique dans toute la suite de ce sujet. (On suppose que f  tan  ). Toute l'étude sera réalisée dans le référentiel lié au laboratoire et supposé galiléen.

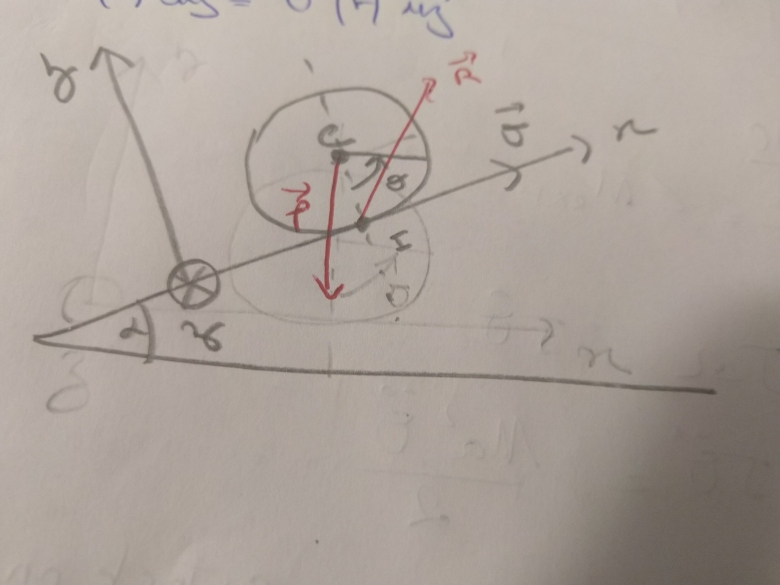
1) Paramétrage de notre roue : Reprendre le schéma suivant sur votre copie en y indiquant l'orientation du repère cartésien Oxyz lié au référentiel du laboratoire et l'angle théta  t repérant la rotation de la roue dans le référentiel du laboratoire de façon que : le vecteur rotation de la roue dans le laboratoire soit :
x t soit l'abscisse du centre d'inertie C de cette roue le long de la ligne de plus grande pente de ce plan incliné. L'axe Ox sera orienté dans le même sens que le vecteur vitesse du tapis roulant.

2) Après avoir défini la vitesse de glissement au niveau du point de contact entre la roue et le sol, montrer qu'elle est telle que v_gl est telle qu'à l'instant initial : v_gl(t=0)=-V<0

vgl/tapis=V (I E roue) - v(I E tapis)

je ne sais pas trop comment continuer

3) On étudie dans cette question le mouvement tant qu'il y a glissement. La réaction du tapis sur la roue sera notée : _xy

a. Montrer que l'application du théorème du centre d'inertie mène aux deux équations suivantes : (1) _x-Mgsin()
(2) : 0=R_y-Mgcos()

TCI :
Bilan des forces : P, R
Projection :
Ox : (1)
Oy : (2)

b. Montrer que l'application du théorème du moment cinétique barycentrique mène à l'équation suivante :
_x (3)

TMC = \frac{dL*}{dt} = \sum{Mext}
L*= J = J
Mext = M_c^pesanteur + M_c^{contact en I}
= 0 + M_I^{contact en I}+R_I .

On dérive L*
Et on trouve (3)

c. Montrer alors que les lois de Coulomb pour le contact entre la roue et le tapis mène à : R(x) fMg x  cos  (4)

d. A l'aide des quatre dernières équations montrer que :
et


On part de (1), on remplace Rx par (4)  puis on intègre et on trouve l'équation demandée.

Pour la 2ème, on part de (3), idem on remplace Rx par (4) puis on intègre et on trouve l'équation demandée.

e. Montrer que la phase de glissement est valide tant que t<t₁ tel que :
t₁=
et vous vérifierez que t₁ >0

f. Exprimer alors  t₁)que l'on notera V1 dans la suite de l'énoncé. Quel est le signe de V1 ?

g. Exprimer alors t  t1  que l'on notera 1 dans la suite de l'énoncé. Quel est le signe de 1 ?

4) On étudie maintenant le mouvement pour t>t1 . On fait maintenant l'hypothèse d'une phase de non-glissement pour t>t1 .

Montrer que :

a. R_x =
et R_y = Mgcos()

b.

c.

d. Valider à la vue des expressions de la question a) précédente l'hypothèse de non glissement de cette deuxième phase du mouvement.