Inscription / Connexion Nouveau Sujet
Mécanique du solide indéformable
Bonjour, je suis face à un exercice de mécanique du solide indéformable et je ne comprend absolument rien, j'ai réellement besoin d'aide, voici l'énoncé.
Soit un disque plein S0 de rayon R et de centre O, de masse m0.
Soit un disque plein S1 de rayon b et de centre O1, de masse m1=m'.
Soit un disque plein S2 de rayon b et de centre O2, de masse m2=m'.
Le disque S3 est composé de S0-S1, donc m3=m0-m'.
Le disque S4 est composé de S0-(S1+S2) donc m4=m0-2m'.
La masse surface p est constante, le repère R est attaché aux solides et R0 est fixé.
Les questions sont les suivantes: ni besoin d'aide pour les 2 première car après le raisonnement est le même mais je ne comprend pas comment il faut faire.
1.Calculer [I0(S0/R)] (détaillée les simplifications et lebclxul des différentes termes de la matrice).
2.Calculer [I01(S1/R)].
3.Calculer [I02(S2/R)].
4.Calculer [I0(S4/R)].
5.Calculer [I0(S4/R)].
6. S3 et S4 sont-ils équilibrés statiquement? Justifier en calculant la position de leurs centre d'inertie respectifs.
7.Pour S3, appliquer le PFD et calculer les termes du torseur statique en O
Je vous joint la photo de la figure ainsi que ce que jai essayer de faire et je vous remercie par avance pour votre aide ?
Bonjour
Il faut d'abord d'intéresser à la matrice d'inertie en O du disque homogène So.
Le moment d'inertie par rapport à Ox est un grand classique : démonstration facile à trouver sur le net :
par raison de symétrie. Donc :
Pas de problèmes pour les produits d'inerties. Ces résultats se transposent facilement aux petits disques S1 et S2. Tu dois aussi connaître la relation de transport d'une matrice d'inertie...
Je te laisse continuer...
Merci beaucoup, il y a zncore quelques petits trucs que je ne comprend pas, j'ai tout noté sur la photo merci encore. 🙂

Si je comprends bien tes difficultés :
1° : le disque homogène So est invariant par rotation autour de l'axe (Ox) ; sa matrice d'inertie en O est la même dans R et dans Ro mais l'énoncé ne la demande pas dans Ro.
2° : pour le petit disque S1, il faut d'abord rechercher sa matrice d'inertie en O1, dans R (ou dans Ro : le résultat est le même). Pour la masse m', il suffit de remarquer que la masse surfacique est une constante :
3° : attention aux relations entre les diverses matrices d'inertie. La soustraction n'est valide que pour des matrices calculées dans le même repère R au même point O. Avant d'effectuer la soustraction, il faut déterminer les matrices d'inerties des deux petits disques en O, pas en O1 et O2... C'est là qu'intervient la relation de "transport" de la matrice d'inertie (théorème de Huygens généralisé).
Je vais regarder a nouveau, et je vais potasser tout ça, merci beaucoup et si jamais j'ai encore des difficultés je reviendrai demain
Merci milles fois 🙂
Bonjour, après avoir refais et refais cet exercice je n'arrive pas à utiliser Huygens, je ne comprend pas comment il faut faire ni comment ça fonctionne 😭
Quelqu'un pourrait-il m'expliquer ?
Merci

Dans un repère donné, la matrice d'inertie en O d'un solide est égale à la matrice d'inertie en G de ce solide augmentée de la matrice en O d'une masse ponctuelle égale à la masse du solide, cette masse ponctuelle étant supposée placée en G. Formule ici :
![]()
Attention : les notations sont à adapter. Les coordonnées dans R de G sont notées (a , b,c) sur le site...
Concernant la matrice d'inertie de S1 en O : plusieurs remarques. Tu n'as pas bien compris le théorème de Huygens. La formule est sur le document fourni en référence.
"m' " apparaît précédé d'un signe +.
Ton expression n'est pas homogène. Tous les termes ont la dimension d'une masse multipliée par le carré d'une distance. Les produits d'inertie sont effectivement nuls mais la diagonale est : a2 , a2 , 0.
Toujours concernant la matrice d'inertie de S1 en O : tu as corrigé une seule des deux erreurs signalées. Pourquoi persister à mettre un signe "-" devant m' ?
Réfléchis aux définitions des moments d'inertie et des produits d'inertie. Ces valeurs, quand elles ne sont pas nulles pour raison de symétrie, sont évidemment plus grandes en O qu'au centre d'inertie.
Oui! Je suis formel! Comme déjà dit : reprends la définition du moment d'inertie par rapport à un axe et examine bien la figure. Il est évident que la distance d'un point quelconque de S1 à l'axe (Ox) est supérieure à sa distance à l'axe (O1x ) : le moment d'inertie de S1 par rapport à (Ox) est supérieur à son moment d'inertie par rapport à (O1x ). Tu peux aussi relire le document dont je t'ai fourni la référence.
Normalement cette fois ci c'est ok, seul bémol pour les centre d'inertie, j'ai beau refaire 100 fois le calcul je trouve 0 de partout 😓

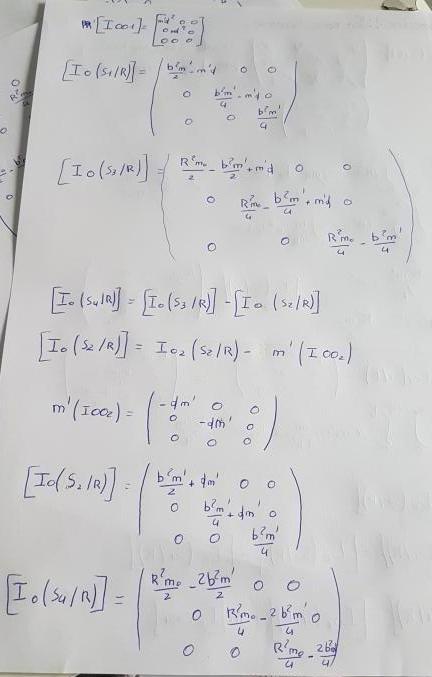

Autant que je puisse en juger, tu n'as pas bien compris le théorème de huygens et il t'arrives d' additionner des termes de dimensions physiques différentes. Je te fournis les trois termes de la diagonale principale de la matrice d'inertie de S1 en O :
m'(a2+b2/2)
m'(a2+b2/4)
m'.b2/4
Concernant les centres d'inertie :
Sans calcul, juste en raisonnant sur les symétries, il est facile de montrer que le centre d'inertie de S et celui de S4 se confondent avec le centre O. Pour S3, on peut traduire en équation le fait que S est la superposition de S1 et de S3.




