Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

mécanique du solide

Posté par
sheigh 21-02-22 à 11:05

Bonjour à tous,

Je souhaiterai avoir quelques explications.

Voici l'énonce de l'exercice:
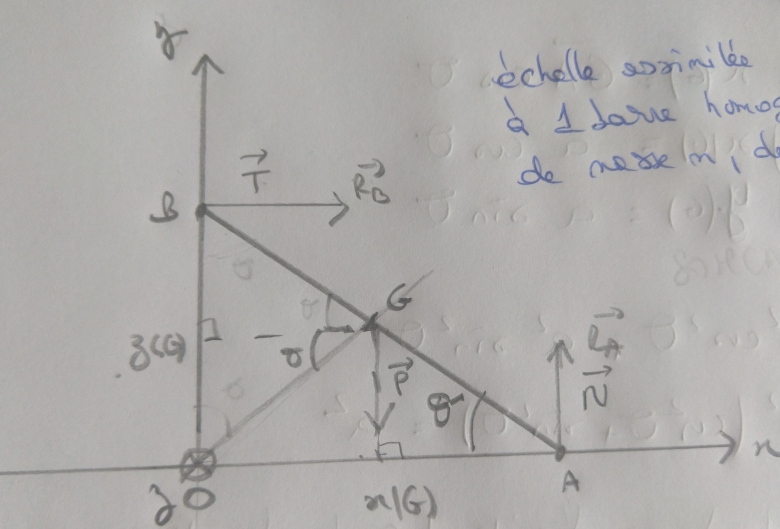
Une échelle AB de masse m , de longueur  2a est assimilée à une barre homogène d'épaisseur négligeable. Elle est en contact sans frottement sur le sol horizontal en A et sur le mur vertical en B. On note Ra  et Rb  les réactions du sol et du mur sur l'échelle. Elle est lâchée sans vitesse initiale pour \theta =\pi /2
  
Voici ce qui me pose problème.
Appliquer les théorèmes du centre d'inertie et du moment cinétique en G. En déduire l'équation différentielle vérifiée par \theta.

TCI:
dP/dt=\Sigma Fext
Projection :
m\ddot{x}(G)=mgasin\theta+Rb (1)
m\ddot{y}(G)=mgacos\theta \+Ra (2)

or x(G)=a cos \theta
alors \ddot{x}(G)=- \ddot{\theta } \dot{\theta }^2 a cos \theta \

de même y(G)= a sin \theta
alors \ddot{y}(G)=-\ddot{\theta }\\\dot{\theta }^2

Qu'on insère dans les expressions 1 et 2 et nous donne Ra et Rb.

Ensuite, TMC:
dL*/dt=\sum{Mext}
\sum{Mext} = MGpesanteur +MGcontact en A+MGcontact en B = Ra\Lambda \vec{GA} + Rb\Lambda \vec{GB}

Je suis complètement embrouillée d'où il me parait difficile de sortir une équation différentielle en \theta Avec le TCI.

Et le L*= J\Omega ^2


Je vous remercie par avance.

Posté par
vanoisere : mécanique du solide 21-02-22 à 11:18

Bonjour
Pour bien fixer les notations et surtout les convention d'orientations et de signes, il faudrait que tu postes un schéma propre où figureraient les différents vecteurs utiles et les orientations des axes.

Posté par
sheighre : mécanique du solide 21-02-22 à 11:27

D'accord, bien sûr, le voici.

mécanique du solide

Posté par
vanoisere : mécanique du solide 21-02-22 à 14:19

Cet énoncé n'est pas très pertinent.
1° : La position =/2 est une position d'équilibre instable. Si on abandonne l'échelle dans cette position sans vitesse initiale, elle y reste ! Il faut donc supposer que l'échelle est abandonnée en =/2 avec une vitesse angulaire non nulle mais très faible (négligeable).
2° : la méthode proposée pour obtenir l'équation différentielle n'est pas la plus simple. En absence de frottement, raisonner sur la conservation de l'énergie mécanique conduit de façon très simple au résultat.
Cela étant dit, on peut quand même s'en sortir par la méthode demandée. Tu as commis quelques erreurs :
1° : au niveau de l'accélération de G :

x_{G}=a.\cos\left(\theta\right)\quad;\quad\dot{x}_{G}=-a.\dot{\theta}.\sin\left(\theta\right)\quad;\quad\ddot{x}_{G}=... \\ \\ z=a.\sin\left(\theta\right)\quad;\quad\dot{z}_{G}=a.\dot{\theta}.\cos\left(\theta\right)\quad;\quad\ddot{z}_{G}=...

Je te laisse finir le calcul ; on obtient dans chaque cas une somme algébrique de deux termes, pas un seul comme tu as écrit.

2° : D'après le théorème de König, il est possible d'appliquer le théorème du moment cinétique par rapport à l'axe de rotation instantanée (Gy) même si le repère barycentrique n'est pas galiléen. Le moment du poids en G étant nul, cela donne :

I_{Gy}.\ddot{\theta}=-R_{A}.a.\cos\left(\theta\right)+R_{B}.a.\sin\left(\theta\right)

Je te laisse continuer. IGy représente le moment d'inertie de la tige par rapport à l'axe (Gy).

Posté par
sheighre : mécanique du solide 21-02-22 à 16:13

Re,

Oolala, j'ai un peu honte je rectifie les dérivées de suite.

Ce qui fait donc :

-ma (\ddot{\theta } sin(\theta )+\dot{\theta ^2} cos(\theta )) = Rb


ma (\ddot{\theta } cos(\theta ) - \dot{\theta ^2} sin(\theta ))+mg = Ra

Ensuite j'ai calculé le moment d'inertie de la tige et ai trouvé J=\frac{ma^2}{3}
donc \frac{dL*}{dt} = \frac{ma^2}{3} \ddot{\theta }

MGext = MGpesanteur+MGcontact en A + MGcontact en B
=0+\vec{Ra} \Lambda \vec{GA} + \vec{\vec{Rb}} \Lambda \vec{GB}

= Ra * a * cos \theta - Rb * a * sin \theta

Je me retrouve avec des signes différents des vôtres, pouvez-vous m'expliquer s'il vous plait.

une fois que je remplace le tout je me retrouve avec une équation que je n'arrive pas à simplifier, il y a de fortes chances d'erreurs :

a cos \theta *[ma (\ddot{\theta } * cos \theta -\dot{\theta ^2}* sin (\theta )=mg]+a*sin \theta [ma(\ddot{\theta } sin\theta +\dot{\theta ^2} cos\theta ] = \frac{ma^2}{3}

Posté par
vanoisere : mécanique du solide 21-02-22 à 18:39

D'accord avec tes expressions de RA et RB.
Pour le théorème du moment cinétique, les signes dépendent de l'orientation de l'angle (non précisée sur ta figure) et donc du sens positif choisi pour la rotation de la tige.
Avec ma convention de signe, la valeur initiale de vaut +/2 . Le sens positif de rotation choisi est le sens des croissant donc le sens de rotation des aiguilles d'une montre. D'où les signes des moments. Avec cette convention, la vitesse angulaire et l'accélération angulaire sont négatives.  Il aurait peut-être été plus pertinent d'appeler l'angle au sommet B. Ainsi on aurait eu à étudier une augmentation de de zéro à/2 ; la vitesse angulaire et l'accélération angulaire auraient été positives ...

Posté par
sheighre : mécanique du solide 22-02-22 à 09:53

Je vous remercie de vos réponses.

J'ai un exercice similaire Tige qui chute le long d'un support horizontal : une tige de masse m, de longueur 2l. On considère qu'il n'y a pas de frottements aux niveaux des supports.
J'ai mis le schéma ci-après.

Comme première question, on doit déduire du théorème de centre d'inertie et le théorème du moment cinétique en G dans le référentiel barycentrique l'équation différentielle vérifiée par \theta.
Et dans la correction, le TCI donne en projection :
m\ddot{x} = 0 maisje ne comprends pas  pourquoi ?

Merci.

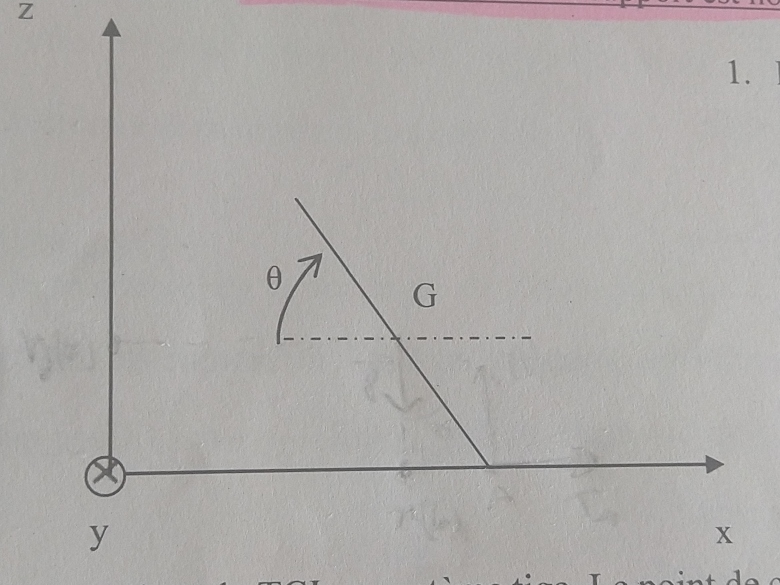
mécanique du solide

Posté par
vanoisere : mécanique du solide 22-02-22 à 11:50

En absence de frottement à l'extrémité inférieure de la tige, la réaction du pan horizontal (Oxy) sur la tige est normale donc verticale. Les deux forces appliquées à la tige sont toutes deux verticales. Donc ?

Posté par
sheighre : mécanique du solide 22-02-22 à 15:18

Ah oui, bien-sûr, \vec{P } et \vec{R}
sont de sens opposés, et s'annulent. J'en oublie les bases qui s'applique aussi dans ce chapitre "mécanique du solide".
Merci beaucoup.  

Posté par
vanoisere : mécanique du solide 22-02-22 à 18:41

Citation :
sont de sens opposés, et s'annulent

"S'annulent" : non  dans la mesure où la projection du vecteur accélération de G suivant (Oz) n'est pas nulle.

Posté par
sheighre : mécanique du solide 22-02-22 à 19:40

Citation :
"S'annulent" : non  dans la mesure où la projection du vecteur accélération de G suivant (Oz) n'est pas nulle.

Je ne comprends pas.

Posté par
vanoisere : mécanique du solide 22-02-22 à 20:59

\overrightarrow{P}+\overrightarrow{R}=m.\overrightarrow{a_{G}}

avec : \overrightarrow{a_{G}}=\ddot{z}_{G}.\overrightarrow{e_{z}}\neq\overrightarrow{0} même si : \ddot{x}_{G}=0

Posté par
sheighre : mécanique du solide 23-02-22 à 08:29

Bonjour,

je vous remercie de cette précision.

Posté par
sheighre : mécanique du solide 23-02-22 à 11:58

Bonjour,

Voici un autre énoncé,
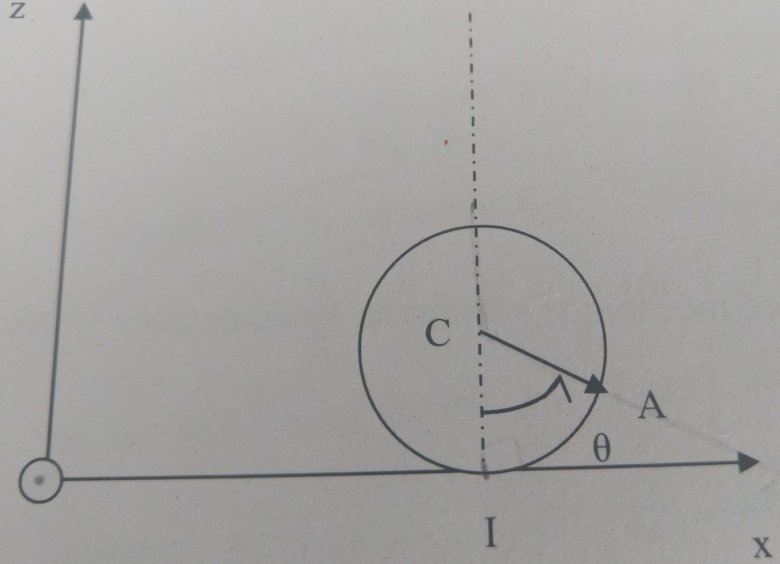
une masse M est fixé en A sur une roue qu'on assimilera à un disque homogène plein de masse m et de rayon R qui roule sans glisser sur un support.  Le schéma est à la suite.

On me demande à partir du théorème de l'énergie mécanique de déterminer l'équation différentielle vérifiée par \theta dans le cadre des petites oscillations.

Voici mon début de procédé :
\frac{dEm}{dt}= PextNC+PintNC
Em=Ec+Epint+Epext


Je calcule en Ec(syt)=Ec(disque)+Ec(A)
Ec(disque)=\frac{1}{2}\dot{\theta }2 (J+mR), il me faudra calculer le moment d'inertie.


Ec(A) = \frac{1}{2} m\vec{v(A))}2
J'utilise Varignon pour le calcul de \vec{v(A))}
qui fait intervenir \vec{CA} :
\vec{v(A)}=\vec{v(C)}+\vec{CA} \ . \vec{\Omega }


d'où : \dot{x(C)} \vec{ux} - \dot{\theta }\vec{uy}\Delta R(cos(\theta ) \vec{ux}+sin(\theta )\vec{uz})
= R\dot{\theta }\vec{ux}+R\dot{\theta }cos(\theta )\vec{uz}+R\dot{\theta }sin(\theta )\vec{ux}
=R\dot{\theta }(1+sin(\theta ))\vec{ux}+ R\dot{\theta } cos(\theta ))\vec{uz}

ensuite je devrais l'insérer dans Ec(A), mais \vec{v(A)} ne me convaincs pas.  Pouvez-vous m'apporter une aide svp, merci.

mécanique du solide

Posté par
vanoisere : mécanique du solide 23-02-22 à 14:09

Remarque préliminaire : si les deux premiers exemples de mouvements étudiés étaient suffisamment proches pour appartenir à un même sujet, il aurait été plus clair pour ceux qui consultent ce forum d'ouvrir un nouveau sujet concernant ce problème...Ce sera pour la prochaine fois...

Pour simplifier l'étude, il serait plus simple de commencer par établir la condition de roulement sans glissement. Cela s'obtient en considérant que le point à la périphérie du disque en contact avec le plan de roulement (cas t=0) est de vitesse nulle par rapport au repère absolu lié au plan de roulement. Cela conduit à une relation simple entre R, \dot{\theta} et Vc.

Pour l'énergie cinétique du disque : connais-tu le théorème de König sur l'énergie cinétique ?

Posté par
sheighre : mécanique du solide 23-02-22 à 17:14

Re,

Je ferai comme demandé pour les prochains exos.

Merci pour vos conseils, les notions sont là mais l'application aux exos faite par le prof est trop brouillonne à mes yeux du coup je m'y perds un peu.

Je vais reprendre votre cheminement, donc :

1- vitesse de Vc grâce au RSG
2- Oui je connais le th de König, il faudra l'utiliser pour l'Ec du disque si j'ai bien compris.

A tout de suite !

Posté par
vanoisere : mécanique du solide 23-02-22 à 19:45

En utilisant la relation de Varignon tu peux établi l'expression générale de A qui va être utile pour l'énergie cinétique. En considérant que cette vitesse est nulle si =0 , on obtient la condition de roulement sans glissement.

Posté par
sheighre : mécanique du solide 24-02-22 à 10:21

Bonjour,

- condition de RSG:
varignon  : \vec{v(C)} = \vec{V(I)} + \Omega . \vec{IC}
la vitesse au point I est nulle car contact avec la surface
d'où \vec{v(C)} = \vec{\Omega } . \vec{IC}
\vec{v(C)} = \dot{\theta }\vec{uy}. -R\vec{uz}

donc condition de RSG = v(C)+\dot{\theta }R=0
\vec{v(C)}=-R\dot{\theta }\vec{ux}


Ec(disque)= Ec*+\frac{1}{2}m v^2(C) (th de König)
avec Ec*= \frac{1}{2} J\Omega ^2 = \frac{1}{2} J \dot{\theta }^2

alors Ec(disque)= \frac{1}{2} J\dot{\theta }^2+\frac{1}{2}m\dot{\theta }^2R^2

Ec(A)=\frac{1}{2} mv^2(A)

et je calcule v(A) avec Varignon et v(C):
\vec{v(A)} = -\dot{\theta }R+\dot{\theta }.\vec{CA}

J'ai un problème de projection pour \vec{CA} = R sin\theta \vec{ux} + R cos\theta \vec{uz} ??

Posté par
vanoisere : mécanique du solide 24-02-22 à 15:20

D'accord avec ta condition de roulement sans glissement. D'accord aussi avec ton expression de l'énergie cinétique du disque. Sachant que le disque est homogène, cette expression se simplifie :

E_{c(disque)}=\frac{3}{4}m.V_{C}^{2}

Concernant la vitesse du point A : les conventions d'orientation choisies sont un peu piégeuses au niveau des signes. Pour ne pas avoir de problème de signes en calculant les produits vectoriels, tu as tout intérêt à utiliser un repère orthonormé direct, ce qui conduit à orienter l'axe (Oy) vers l'arrière du plan de figure. Compte tenu du sens positif de rotation précisé sur le schéma, cela conduit à poser :

\overrightarrow{\Omega}=-\dot{\theta}.\overrightarrow{u_{y}}

ce qui conduit à une vitesse de A dans le repère (Oxyz) :

\overrightarrow{V_{(A)}}=\overrightarrow{V_{(C)}}+\overrightarrow{\Omega}\wedge\overrightarrow{CA}=R.\dot{\theta}.\left[\left(\cos\left(\theta\right)-1\right).\overrightarrow{u_{x}}+\sin\left(\theta\right).\overrightarrow{u_{z}}\right]

En élevant au carré (je saute quelques intermédiaires de calculs) :

V_{A}^{2}=2V_{C}^{2}\cdot\left[1-\cos\left(\theta\right)\right]

Remarque : tu peux constater que ces résultats sont bien cohérents avec le fait que la vitesse de A s'annule en \theta=0.

Posté par
sheighre : mécanique du solide 25-02-22 à 15:57

Bonjour,

Je vous remercie. Cependant j'ai encore quelques soucis :

de signe, je trouve \vec{V(A)}=\dot{\theta }R\vec{ux}-R\dot{\theta }sin(\theta )\vec{uz}+R\dot{\theta }cos(\theta )\vec{ux}
ce qui n'est pas vraiment votre formule car vous obtenez un signe - pour le sinus.

Aussi pouvez-vous me détailler comment êtes-vous arriver à trouver cette forme de v^2(A) car je n'arrive pas non plus au même résultat.

Puis j'ai continué :

Epint=0; PNCint=0

Epext=Ep(disque)+Ep(A)=mgz(C)+mgz(A)=mgR+MgRcos(\theta
)

PNCext=PNCcontact en I=RI.\vec{v(I)}+\vec{\Omega }.MI=0 car MI=O contact ponctuel en I et \vec{v(I)}=0 car RSG.

d'où \frac{d(Ec+Ep)}{dt}=0

Il me restera à tout regrouper pour avoir je l'espère l'équation différentielle demandée.

Posté par
vanoisere : mécanique du solide 25-02-22 à 19:25

La vitesse de A s'annule nécessairement en  =0. Ton expression est donc fausse. Il y a plusieurs pièges au niveau des signes  :
Vitesse de  C égale à -R'.
Orientation du vecteur rotation instantanée...
Pour le carré de la vitesse  : tu as juste à remarquer la somme du carré d'un sinus et du carré du cosinus du même angle...
Puisque la vitesse de I considéré comme appartenant au disque est nulle, la puissance instantanée de la réaction est nulle à chaque instant. La réaction ne travaille pas. Pas de difficulté donc pour l'énergie mécanique.

Posté par
sheighre : mécanique du solide 28-02-22 à 21:52

merci, je vais reprendre cela posément.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !