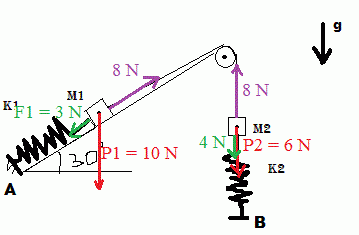
Calculer P1 = m1.g = 10 N
et F1 = k1 * (AM1 - L1) = ... = 3 N
Calculer alors la force de la corde sur M1 pour que M1 soit en équilibre ... tu devrais trouver 8 N

Calculer P2 = m2.g = 6 N
La tension du fil (8N) est aussi appliquée sur M2
On calcule alors F2 (force du ressort 2 sur M2) pour que M2 soit en aquilibre, on trouve F2 = 8-6 = 2 N

et avec F2 = k2.(BM2 - L2) = ... = 2 N

2 = k2 * (0,32 - 0,30) = 0,02 k2

k2 = 100 N/m
-----
Sauf distraction.  

Merci beaucoup

La deuxieme partie:
Si On tire la masse M2 vers le Bas d'une longueur H=1cm à partir de la position d'équilibre, puis on abandonne le système à t=0 sans vitesse initiale.
on demande de :
- ecrire les equations de mouvement M1 et M2.
-Montrer que le systeme effecture un mouvement oscillatoire. Calculer la periode des oscillations
-Quelle est la position de M2 par rapport à B à t=10s

Merci

-M1=1kg et M2=600g
-La masse M1 peut glisser sans frottement
-la constante de raideur K1=50 N/m
-le Fil qui passe à travers la poulie est inextensible et a une masse negligeable.
- la poulie est sans masse
- le champs de pesanteur g= 10 m/s²

Si On tire la masse M2 vers le Bas d'une longueur H=1cm à partir de la position d'équilibre, puis on abandonne le système à t=0 sans vitesse initiale.
on demande de :
- ecrire les equations de mouvement M1 et M2.
-Montrer que le systeme effecture un mouvement oscillatoire. Calculer la periode des oscillations
-Quelle est la position de M2 par rapport à B à t=10s



*** message déplacé ***

Bonjour,

Rappel : le multi-post n'est pas toléré dans ce forum.
 

-M1=1kg et M2=600g
-La masse M1 peut glisser sans frottement
-la constante de raideur K1=50 N/m
-le Fil qui passe à travers la poulie est inextensible et a une masse negligeable.
- la poulie est sans masse
- le champs de pesanteur g= 10 m/s²

Si On tire la masse M2 vers le Bas d'une longueur H=1cm à partir de la position d'équilibre, puis on abandonne le système à t=0 sans vitesse initiale.
on demande de :
- ecrire les equations de mouvement M1 et M2.
-Montrer que le systeme effecture un mouvement oscillatoire. Calculer la periode des oscillations
-Quelle est la position de M2 par rapport à B à t=10s



*** message déplacé ***

Energie mécanique du système = constante :

1/2 k2 . (Delta L2)² + 1/2 k1 . (Delta L1)² - m2.g.x - m2.g.x.sin(30°) + (m1 + m2).v² = constante. (avec v la vitesse des masses)

50 * (0,02 + x)² + 25 * (0,06+x)² - x + 0,8.v² = constante

On dérive par rapport au temps :

100 * (0,02 + x).dx/dt + 50 * (0,06 + x).dx/dt - dx/dt + 1,6.v.dv/dt = 0

et avec v = dx/dt --->

100 * (0,02 + x) + 50 * (0,06 + x) - 1 + 1,6.dv/dt = 0

100 * (0,02 + x) + 50 * (0,06 + x) - 1 + 1,6.d²x/dt² = 0

4 + 150x + 1,6 d²x/dt² = 0

d²x/dt² + 93,75.x + 2,5 = 0

Avec x(0) = 0,01 et (dx/dt)(0) = 0

p = +/- i*V(93,75) = +/- 9,68.i

x(t) = A.sin(9,68.t) + B.cos(9,68.t) - 0,0267

x(0) = 0,01 --> B = 0,0367

(dx/dt)(0) = 0 ---> 9,68.A = 0 --> A = 0

x(t) = 0,0367.cos(9,68.t) - 0,0267 (avec t en s et x en m)

Si on veut x en cm, alors : x(t) = 3,67.cos(9,68.t) - 2,67

w = V(93,75) rad/s = 2Pi/T
T = 2Pi/V(93,75) = 0,649 s (arrondi)
-----

Sans aucune vérification ... il faut les faire.

bjr
Pourquoi on prend l'energie potentiel du à la pesenteure en negatif
"*** 1/2 k2 . (Delta L2)² + 1/2 k1 . (Delta L1)² - m2.g.x - m2.g.x.sin(30°) + (m1 + m2).v² = constante. (avec v la vitesse des masses) ****"

Correction, faute de frappe et erreur de signe :


Dans ma réponse, remplacer :1/2 k2 . (Delta L2)² + 1/2 k1 . (Delta L1)² - m2.g.x - m2.g.x.sin(30°) + (m1 + m2).v² = constante.

par 1/2 k2 . (Delta L2)² + 1/2 k1 . (Delta L1)² - m2.g.x + m1.g.x.sin(30°) + (1/2).(m1 + m2).v² = constante.

Et continuer comme suit :

50.(0,02 + x)² + 25.(0,06 - x)² - 0,6*10*x + 1*10.x/2 + (1/2)*1,6.v² = constante.

50.(0,02 + x)² + 25.(0,06 - x)² - 6*x + 5.x + 0,8.v² = constante.

50.(0,02 + x)² + 25.(0,06 - x)² - x + 0,8.v² = constante.

On dérive par rapport au temps :

100.(0,02 + x) dx/dt + 50.(0,06 - x) dx/dt - 1 + 1,6.v dv/dt = 0

et avec v = dx/dt --->

100.(0,02 + x) + 50.(0,06 - x) - 1 + 1,6 dv/dt = 0

2 + 100x + 3 - 50x - 1 + 1,6 dv/dt = 0

1,6 d²x/dt² + 50x + 4 = 0

d²x/dt² + 31,25.x  = - 2,5

x(t) = -2,5/31,25 + A.sin(5,59.t) + B.cos(5,59t)

x(t) = -0,08 + A.sin(5,59.t) + B.cos(5,59t)

x(0) = 0,01 ---> 0,01 = -0,08 + B ; B = 0,09

x(t) = -0,08 + A.sin(5,59.t) + 0,09.cos(5,59t)

(dx/dt)(0) = 0
5,59.A = 0 ---> A = 0

x(t) = 0,09.cos(5,59t) - 0,08 (avec t en s et x en m)

Si on veut x en cm :

x(t) = 9.cos(5,59t) - 8

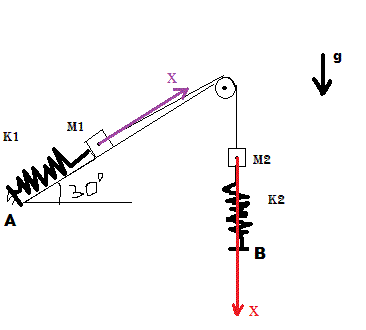
Qui donne l'équation du mouvement des 2 masses.

Avec l'axe des x en rouge pour M2 et l'axe des x en mauve pour M1.
L'origine de ces axes est au centre d'inertie des masses lorsque le système est au repos.



-----
Sauf nouvelle distraction.  

Zut et rezut.
Encore erreur de signe .

1/2 k2 . (Delta L2)² + 1/2 k1 . (Delta L1)² - m2.g.x + m1.g.x.sin(30°) + (1/2).(m1 + m2).v² = constante.

Et continuer comme suit :

50.(0,02 - x)² + 25.(0,06 + x)² - 0,6*10*x + 1*10.x/2 + (1/2)*1,6.v² = constante.

...