Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

Mécanique du solide

Posté par
phisics-girl 27-11-09 à 17:42

Bonjour,
J'ai besoin de votre aide pur résoudre cet exercice.

Une barre AB, homogène, de longueur 2.l est mobile relativement à un repère R0(o,x0,y0,z0). L'extrimité A est mobile sur le plan (0,x0,y0) et l'exrimité B est mobile sur l'axe (o,z0) : AB = 2.l.z ( voir la figure )
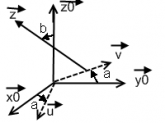
Mécanique du solide

1/ Déterminer les éléments de réduction du torseur cinématique au point B,
2/ Calculer l'accélération du point A
3/ Déterminer l'axe central de ce torseur,
Si le point A est astreint à se déplacer sur l'axe (o,y0)
4/Déterminer l'axe central du torseur cinématique,
5/Déterminer la base et la roulante,
6/En déduire les axoides du mouvement de la barre dans R0

**************

Mes essais :

J'ai effectué les angles d'Euler
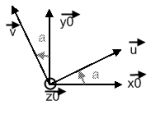
Mécanique du solide
et
Mécanique du solide

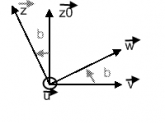
et ainsi on peut conclure que :
(S/R0)= (dérivée de a) . z0+(dérivée de b)

Je ne peux pas continuer si c'est pas correcte.
Salut et merci d'avance

Edit Coll : images placées sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
phisics-girlre : Mécanique du solide 27-11-09 à 18:51

J'ai vraiment besoin de votre aide
est-ce que déja l'expression du vecteur  , la résultante générale, est correcte?
Merci

Posté par
donaldosre : Mécanique du solide 27-11-09 à 20:45

Ça  a l'air correct.

Posté par
phisics-girlre : Mécanique du solide 27-11-09 à 23:35

Okay, merci.
Pour la seconde question, comment le faire?

Posté par
donaldosre : Mécanique du solide 28-11-09 à 10:59

Puisque tu as entièrement déterminé le torseur cinématique au point B, tu peux l'utiliser pour en déduire l'expression de la vitesse en A.

Il ne te reste ensuite qu'à dériver cette expression.

Posté par
phisics-girl) 28-11-09 à 19:32

salut,
J'ai effectué le calcul de deux manières ,mais que qui m'énervec'est que je n'arrive pas au même résultat..
effectivement j'ai utilisé la relation du champs de vecteur d'un torseur.
Ainsi j'ai
d(OA)/dt|R0 =d(OB)/dt|R0 +(R/R0)BA

On a BA = -2l.Z , (R/R0) = b.+a.Z0 , d(OB)/dt=-2l.[d(b)/dt].sin(b). Z0

Donc,
d(OA)/dt)|R0 = -2.l.[d(a)/dt].sin(b). +2.l.[d(b)/dt].cos²(b).-l.[d(b)/dt].sin(2b).Z
d²(OA)/dt²|R0= d(d(OA)/dt|R0)|R + (R/R0)d(OA)/dt|R0
d(d(OA)/dt|R0)|R = (-2.l.d²a/dt².sinb-2.l.da/dt.cos b )
+(-4.l.db/dt.sin b . cos b +2.l.d²b/dt².cos²b)
+(-l.d²b/dt².sin(2b) - 2.l.db/dt . cos(2b)

(R/R0)d(OA)/dt|R0 = -2l.(da/dt.db/dt.sin²b.cos b + da/dt.db/dt.cos²b.cos)+
2.l(db/dt.sin(b).cos(b)-da/dt.cos(b).sin(b) )+
2.l( (db/dt)².cos²b+(db/dt)².sin²b).Z

et ainsi on fait la somme...
Par contre,
En applicant la relation directe pour calculer l'accélérationb :
a(A/R0) = ar(A)+ ae(A)+ ac(A)
il me semble que B est l'originie du repère R , la chose qui ma permis de conclure que :
ar(A) = d²(BA)/dt²|R = 0 ( parce que B et A sont fixe dans R )
ae(A)=d [(R/R0)]/dt|R0BA
ac(A)=2.(R/R0)dBA/dt|R

a(A/R0) = 2.l. d²(a)/dt²|R0 . sin(b).-2.l.(d²(b)/dt²|R0 +(d(a)/dt|R0)² .sin(b).cos(b). + 2.l.(d()/dt|R0)²+2.l.(d(a)/dt|R0)².sin²b . Z

Ainsi, je n'obtiens pas le même résultat...
une faute dans le calcul? je ne sais pas..
SVP, j'ai vraiment besoin de votre aide,..
Veuillez vérifier le calcul avec moi.
Merci!!

Posté par
phisics-girlre : Mécanique du solide 28-11-09 à 22:36

SVP, j'ai tellement besoin d'aide, si c'est fatigant à rédiger vous pouvez scanner votre  brouillon et le poster sur le forum,..
Merci d'avance!

Posté par
donaldosre : Mécanique du solide 29-11-09 à 12:00

C'est déjà fatiguant à lire

Plus sérieusement, je n'ai lmalheureusement le temps de reprendre tes calculs, je le ferai peut-être ce soir.

LCe que je peux dire c'est que les deux approches sont correctes. Cependant le point A est contraint à se déplacer dans le plan (O,\vec{u},\vec{v}), l'accélération doit donc y être contenue (pas de composante verticale...).

Ton expression de l'accélération d'entraînement  me semble par ailleurs incorrecte.


Pour une approche simple et éviter trop de produits vectoriels, tu peux poser dans un premier temps \vec{OA}=\rho \vec{v} et dériver en te ramenant à un problème dans le plan horizontal. Tu pourras ensuite remplacer \rho et ses dérivées en partant de \rho=2l\sin b.

J'essaierai de poster mes résultats pour les différentes approches plus tard.

Tu peux toujours continuer l'exercice.

Posté par
phisics-girlre : Mécanique du solide 29-11-09 à 12:45

Bonjour,
Ah, oui, vous avez raison concernant l'accélération d'entraiement, j'ai oublié l'expression de l'accélération du point coincidant : d²OB/dt²
J'ai vérifié ici
http://upload.wikimedia.org/math/0/3/1/0315b740f47c411807376aeb502c0f3e.png
( à Wikipédia A est l'origine du repère relatif et M le point mobile )
concernant l'accélération plane, pour mes calculs j'ai projeté dans la base (0,,,Z) , c'est pour cela il y aura de composante suivant Z, mais biensur nulle suivant Z0 .
Merci, espérant que tu pourras me refaire le calcul ce soir.
Merci encore

Posté par
phisics-girlre : Mécanique du solide 29-11-09 à 13:30

Merci pour ta méthode, je viens juste d'obtenir ceci :
http://img7.hostingpics.net/pics/352164A.gif
consuler le lien ( je viens de remarquer la remarque de ne pas poster des images sur le forum pour ne pas l'alourdir).

Mais je suis encore intéressée aux deux autres méthodes.
Merci beaucoup!

Posté par
donaldosre : Mécanique du solide 29-11-09 à 19:33

1. en posant \vec{OA}=\rho \vec{v}

\left.\frac{{\rm d}\vec{OA}}{{\rm d}t}\right|_{\mathcal{R}_0}=\dot{\rho}\vec{v}-\rho\dot{a}\vec{u} \\

et

\left.\frac{{\rm d}^2\vec{OA}}{{\rm d}t^2}\right|_{\mathcal{R}_0}=-\left(2\dot{a}\dot{\rho}+\rho\ddot{a}\right)\vec{u}+\left(\ddot{\rho}-\rho\dot{a}^2^\right)\vec{v} \\

sachant que

\left\{\begin{array}{rcl} \rho&=&2l\sin b \\ \dot{\rho}&=&2l\dot{b}\cos b \\ \ddot{\rho}&=&2l\left(\ddot{b}\cos b-\dot{b}^2\sin b\right)\end{array}\right.

ce qui doit donner au final:

\left.\frac{{\rm d}^2\vec{OA}}{{\rm d}t^2}\right|_{\mathcal{R}_0}=-2l\left(2\dot{a}\dot{b}\cos b+\ddot{a}\sin b\right)\vec{u}+2l\left(\ddot{b}\cos b-\dot{b}^2\sin b-\dot{a}^2\sin b\right)\vec{v} \\

(les accents graves sont censés être des points mais ils sont mal rendus, ils représentent bien sûr la dérivation par rapport au temps)

Posté par
donaldosre : Mécanique du solide 29-11-09 à 19:38

Cette technique revient en fait à travailler dans le repère intermédiaire \mathcal{R}'=\left( 0,\vec{u},\vec{v},\vec{z_0}\right) avec \vec{\Omega}_{(\mathcal{R}'/\mathcal{R}_0)}=\dot{a}\vec{z_0}.

Posté par
donaldosre : Mécanique du solide 29-11-09 à 20:58

Concernant la formule de composition des accélérations, tu as pu constater qu'elle se résume à l'accélération d'entraînement:

\fbox{\left.\frac{{\rm d}^2\vec{OA}}{{\rm d}t^2}\right|_{\mathcal{R}_0}=\left.\frac{{\rm d}^2\vec{OB}}{{\rm d}t^2}\right|_{\mathcal{R}_0}+\left.\frac{{\rm d}\vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}}{{\rm d}t}\right|_{\mathcal{R}_0}\times \vec{BA} + \vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}\times\left(\vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}\times \vec{BA}\right)}

avec

\fbox{\left.\frac{{\rm d}^2\vec{OB}}{{\rm d}t^2}\right|_{\mathcal{R}_0}=-2l\left(\ddot{b}\sin b + \dot{b}^2 \cos b\right)\quad \vec{z_0}}

\left.\frac{{\rm d}\vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}}{{\rm d}t}\right|_{\mathcal{R}_0}=\ddot{a}\vec{z_0}+\ddot{b}\vec{u}+\dot{b}\dot{a}\vec{v}
\\ \\ et \\ \\ \vec{BA}=-2l\vec{z}=-2l\left(\cos b \quad\vec{z_0}-\sin b \quad\vec{v}\right)

d'où, après avoir effectué les produits vectoriels:

\fbox{\left.\frac{{\rm d}\vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}}{{\rm d}t}\right|_{\mathcal{R}_0}\times \vec{BA}=-2l \left(\ddot{a}\sin b+\dot{a}\dot{b}\cos b\right)\quad\vec{u}+2l\ddot{b}\cos b\quad\vec{v}+2l\ddot{b}\sin b\quad \vec{z_0}}

et enfin:
, après de nouveaux calculs plus trépidants les uns que les autres :

\fbox{\vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}\times\left(\vec{\Omega}_{(\mathcal{R}/\mathcal{R}_0)}\times \vec{BA}\right)=-2l\left(\dot{a}\dot{b}\cos b \quad \vec{u}+\left(\dot{b}^2 \sin b + \dot{a}^2 \sin b\right) \quad \vec{v}-\dot{b}^2\cos b \vec{z_0}\right)}

En additionnant les trois termes ci-dessus, la composante selon \vec{z_0} doit disparaître et l'on doit obtenir l'expression de l'accélération de A (de préférence identique à l'expression trouvé dans mon précédent message, mais je te laisse vérifier...).

Posté par
phisics-girlre : Mécanique du solide 03-12-09 à 19:23

Ah, vraiment je te remercie pour ton grand effort afin de m'aider, Donaldos!!!
Merci, merci, merciiiiiiiii

Posté par
sweetylovlysalut 07-12-09 à 00:36

salut
j'ai vraiment besoin de corrige cette exercice, la corrigé complet ou corrigé lien peut m'aider
parce que j'a un controle le 8-12
ne oublie  moi
et merci a tous


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !