Inscription / Connexion Nouveau Sujet
Mécanique du point Propulsion par un ressort
Bonjour,
On me propose l'énoncé suivant:
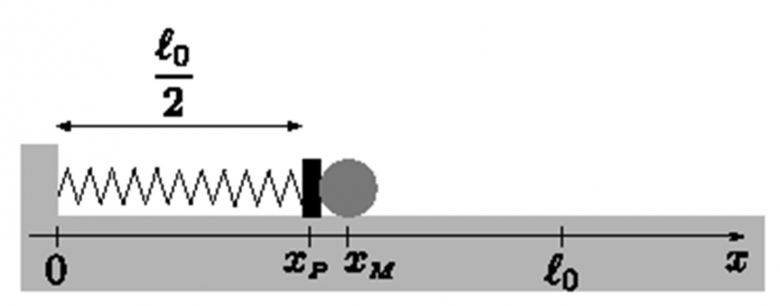
"M va être propulsé par une plaque P, de masse mp >> m, que l'on traitera comme un point matériel. Cette plaque est située à l'extrémité d'un ressort de raideur k et de longueur vide L0. Dans l'état initial (voir figure), le ressort est comprimé à une longueur, L0/2 et M est placé en contact avec P. À t=0 on lâche P sans vitesse. On néglige les frottements de P et M avec la piste."
La situation est schématisée sur l'image attachée.
1) Faire le bilan des forces qui s'exercent sur M.
2) Que peut-on dire de l'énergie mécanique du système {M + P + ressort + Terre}
3) Déterminer par un raisonnement énergétique la vitesse de M à l'instant où il rompt le contact avec P en fonction de m, k et L0.
4) Quelle est sa vitesse ultérieure?
5) En déduire en fonction Vam la valeur de L0 pour que le point M passe par A
avec la vitesse minimale Va qui lui permet de quitter la piste à son sommet.
Pour la 1ère question:
Les forces qui s'exercent sur M sont, le Poids, la force élastique du ressort et la réaction de la piste.
Voilà un schéma que j'ai réalisé.
Cependant, j'ai un doute:
Pour la force élastique du ressort, faut-il que je dise que cette force s'applique sur P et ensuite "P l'applique sur M" ou puis-je dire directement que la force du ressort s'applique sur M?
Quant à la question 2:
Le travail du poids et de la réaction du support s'annulent.
Seul la force élastique du ressort travaille sur l'ensemble du système.
La force élastique est conservative. Donc l'énergie mécanique du système est constante.
Est-ce bien cela?
Par contre je bloque un peu sur la question 3, je ne vois pas vraiment comment utiliser les informations pour répondre.
Ce que je sais c'est que M rompt le contact avec P au moment où xP = L0. Mais je ne sais pas comment aller plus loin.
Ce que je sais c'est que:
 Em = 0
Em = 0
Or  Em =
Em =  Ec +
Ec +  Ep
Ep
L'altitude ne varie pas donc:  Ep = 0
Ep = 0
Est-ce correct? J'essaie d'avancer à partir de là
On me demande d'exprimer la vitesse en fonction de m, k et L0. Pour avoir k et L0, je suppose qu'il va falloir que je fasse intervenir le travail de la force élastique du ressort mais je ne vois pas vraiment comment amener cela ^^
L'altitude ne varie pas donc:
 Ep = 0
Ep = 0 Tu oublies l'énergie potentielle élastique du ressort.
Ah oui merci pour l'indication.
Ep(xP) = (k/2) * (L0/2 - L0)^2 = kL0^2/8
Ec(Lo) = 1/2mVL0^2
 Em =
Em =  Ec +
Ec +  Ep = 0
Ep = 0
On a donc:
1/2mVL0^2 = kL0^2/8
mVL0^2 = kL0^2/4
VL0^2 = kL0^2/4m
VL0 = sqrt(kL0^2/4m)
Est- ce bien cela?
OK. Pour être rigoureux, il faudrait justifier pourquoi le contact entre M et P cesse quand le ressort retrouve sa longueur à vide.
Pour justifier cela:
P est située à l'extrémité du ressort qui a une longueur à vide L0. À t=0, on lâche P sans vitesse mais on ne "tire pas sur le ressort", celui-ci revient donc à sa longueur à vide. C'est à ce moment que M rompt avec P.
Je ne sais pas si c'est très rigoureux ^^
C'est à ce moment que M rompt avec P.
C'est justement cela qu'il faut montrer. La première question peut aider...
Faudrait-il que je dise que la force que P exerce sur M s'annule en L0:
La force exercé par le ressort sur P est: F = -k(x-L0)Ux avec x la longueur du ressort à l'instant t. Donc au moment ou x = L0, F = 0. Donc F n'exerce plus de force sur P et P n'exerce plus de force sur M.
Est-ce bien cela?
Faudrait-il que je dise que la force que P exerce sur M s'annule en L0:
C'est bien cela mais il faut le montrer !
Selon la question 1, puisque le poids de M est compensé par la réaction verticale de la piste (absence de frottement), la RFD appliquée à M conduit à :
où
Puisque m<<mP, le plateau a pratiquement même mouvement, qu'il soit en contact ou pas avec M. La RFD appliquée au plateau conduit , en projection sur l'axe des x :
-k(xP-Lo)=mp.a
On voit bien ainsi que le vecteur accélération s'annule pour changer de sens pour xP=Lo.
Merci, c'est très clair ainsi !
Pour la question 4, je vais re-attaché le schéma entier du problème:
On néglige les frottements de M avec la piste.
Entre L0 et A, la somme des forces qui s'appliquent sur M est nulle. Le mouvement est donc uniforme et VL0 = Va.
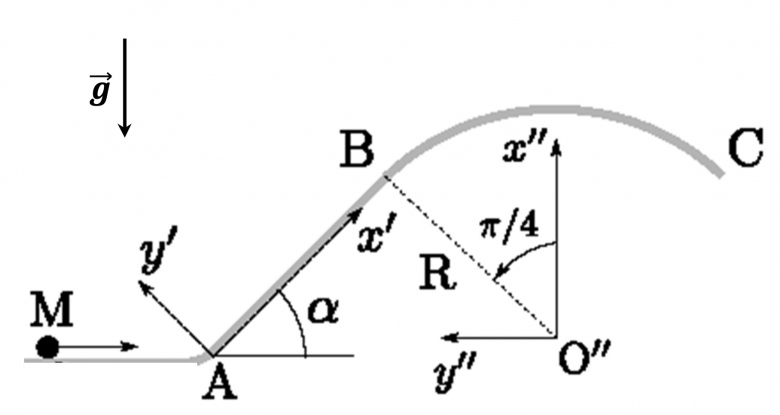
Pour la question 5:
Le mouvement est uniforme entre L0 et A.
Ainsi, pour que le point M passe par A avec la vitesse minimale Vam qui lui permet de quitter la piste à son sommet, il faut que:
VL0 = Vam
sqrt(kL0^2/4m) = Vam
KL0^2/4m = Vam^2
kL0^2 = 4mVam^2
L0^2 = 4mVam^2/k
L0 = sqrt(4mVam^2/k)
Le raisonnement est correct. J'ai laisser passer une étourderie de notation. La conservation de l'énergie mécanique entre l'instant initial et l'instant ou M quitte le plateau conduit à :
Il te reste juste à remplacer m par mp dans tes derniers messages.
Faut-il que j'utilise m ou mp? Car dans les données qui nous sont communiquées à la fin, nous n'avons pas la valeur de mp. Nous avons uniquement la valeur de m.
** image supprimée **
Je persiste : la conservation de l'énergie mécanique conduit bien à :
Peut-être y a-t-il une faute de frappe dans l'énoncé tel que tu l'as copié et faut-il lire :
mp<<m ? Cela me paraîtrait d'ailleurs plus vraisemblable que mp>>m...
Je crois bien que c'est une erreur dans l'énoncé, je vais contacter mes professeurs (en espérant que ceux-ci me répondent. Je suis étudiant à distance et le temps des réponses est...).
Dans le cas où mp << m, je pourrais donc garder ce que j'ai écris?
J'ai juste une dernière question concernant la détermination de l'expression de Vam, la vitesse minimale de A pour que M quitte la piste au sommet.
À la fin de la première partie du problème, qui a été traité dans le sujet intitulé "Mécanique du point plan incliné".
J'obtiens la vitesse de M en B:
Vb = sqrt(Va^2 - gsqrt(2)L(1+ d))
d))
Dans le sujet intitulé "Mécanique du point base polaire portion de cercle", nous avons déterminé la vitesse minimum que M devrait avoir en B pour pouvoir quitter la piste à son sommet:
Vb >= sqrt(Rg(3-sqrt(2))
Pour trouver Vam, j'ai donc raisonné ainsi:
Bonsoir,
@Jawad0610 : ne pas abuser des insertions d'image pour du texte, tu as tout ce qu'il faut pour faire autrement :
Toutes mes excuses, gbm, j'utiliserai les images de manières plus consciencieuses à l'avenir.
Serait-il possible de savoir si mon expression de Vam est correcte?
Dans le cas où mp << m, je pourrais donc garder ce que j'ai écris?
oui !
Ton dernier calcul est correct.
Dans ce cas, il ne me reste plus qu'a vous remercier infiniment pour l'aide que vous m'avez apporter dans la résolution de ce problème. 
C'est encore moi ^^.
Je faisais l'application numérique et j'ai l'impression qu'il y a un couac.
On nous demande de donner les valeurs numériques de Vam, Vb et L0.
Les données que l'on nous donne sont les suivantes:
 s = 0,3 ;
s = 0,3 ;  d = 0,1 ; m = 100g ; L = 50 cm ; R = 30 cm ; k = 25 N/m et g = 10 m/s^2
d = 0,1 ; m = 100g ; L = 50 cm ; R = 30 cm ; k = 25 N/m et g = 10 m/s^2
Valeur de Vam:
On a déterminé l'expression suivante:
Vam = sqrt( g ( R (3 - sqrt(2) ) + L (1 +  d ) ) )
d ) ) )
En remplaçant, j'obtiens Vam = 3,2 m/s
En me basant sur ce résultat, j'essaie d'obtenir la valeur de Vb:
On sait que:
Vb = sqrt( Vam^2 - g sqrt(2) L (1+ d))
d))
En remplaçant, j'obtiens Vb = 1,57 m/s
Or, Vam est censé être la vitesse minimale de M en A pour que M puisse quitter la piste au sommet de la trajectoire.
Pour que M puisse quitter la piste au sommet de la trajectoire, nous avons déterminé qu'il faut que:
Vb > sqrt(R g (3 - sqrt(2))
Or sqrt(R g (3 - sqrt(2)) = 2.18 m/s.
On a donc Vb < sqrt(R g (3 - sqrt(2)) (avec la valeur Vam = 3.2 m/s)
Je ne vois vraiment pas où est l'erreur, auriez-vous une idée? ^^
J'avais tout simplement oublié un sqrt(2) dans l'expression de Vam.
Je trouve donc:
Vam = 3.54 m/s
Vb = 2.18 m/s (qui vérifie donc bien Vb  sqrt(R g (3 - sqrt(2)) )
sqrt(R g (3 - sqrt(2)) )
L0 = sqrt(4mVam^2/k) ; En remplaçant, j'ai: L0 = 40 cm.
Il va falloir que j'apprenne à être plus rigoureux, même sur des problèmes relativement long comme celui-ci.
Encore une fois, merci pour votre aide.
Bonjour vanoise 
J'ai reçu une réponse de la part de ma professeure concernant la question sur mp >> m.
Elle m'a répondu qu'il n'y a pas d'erreur. On a bien mp >> m et elle m'a aussi dit que l'on utilise pas mp que ce soit dans les expressions ou dans les applications numériques.
Donc, quand je fais ce calcul, puis-je garder Ec(L0) = 1/2mVL0^2 ?
Ah oui merci pour l'indication.
Ep(xP) = (k/2) * (L0/2 - L0)^2 = kL0^2/8
Ec(Lo) = 1/2mVL0^2
 Em =
Em =  Ec +
Ec +  Ep = 0
Ep = 0
On a donc:
1/2mVL0^2 = kL0^2/8
mVL0^2 = kL0^2/4
VL0^2 = kL0^2/4m
VL0 = sqrt(kL0^2/4m)
Est- ce bien cela?
Il faut être très clair et essayer de réfléchir tout en faisant preuve d'esprit critique...
Dans la phase de poussée du ressort, il s'agit bien de l'ensemble {M-P} qui passe de la vitesse nulle à la vitesse VLo. C'est donc bien cet ensemble de masse (m+mp) qui voit son énergie cinétique augmenter par diminution de l'énergie potentielle élastique du ressort. Nous avons donc de façon incontestable comme écrit dans mon message du 04-03-20 à 19:10 :
Donc, en toute rigueur : la vitesse VLo dépend de la somme (m+mp).
Reste ensuite les approximations possibles . Il y en a deux :
1. La plus vraisemblable : une faute de frappe dans l'énoncé et mp<<m ; dans ces conditions, VLo et tous les résultats suivants ne font plus intervenir mp ; seul m intervient dans les résultats.
2. Pas d'erreur d'énoncé : mp>>m et alors VLo dépend de mp ; la suite du problème ne faisant intervenir évidemment que la masse m.
Mais bon : l'essentiel est que tu comprennes bien la résolution du problème ! Cette histoire de simplification n'est qu'un détail ! 
J'ai l'impression que mp >> m a été précisé pour être utilisé dans ce raisonnement:
Faudrait-il que je dise que la force que P exerce sur M s'annule en L0:
C'est bien cela mais il faut le montrer !
Selon la question 1, puisque le poids de M est compensé par la réaction verticale de la piste (absence de frottement), la RFD appliquée à M conduit à :
où
Puisque m<<mP, le plateau a pratiquement même mouvement, qu'il soit en contact ou pas avec M. La RFD appliquée au plateau conduit , en projection sur l'axe des x :
-k(xP-Lo)=mp.a
On voit bien ainsi que le vecteur accélération s'annule pour changer de sens pour xP=Lo.
2. Pas d'erreur d'énoncé : mp>>m et alors VLo dépend de mp ; la suite du problème ne faisant intervenir évidemment que la masse m.
Mais que faire alors dans ce cas-là?
Comment faire pour que la suite du problème ne fait intervenir uniquement que la masse m?
Dois-je considérer une Ec à un autre point ?
Je pense avoir été clair : s'il n'y a pas d'inversion dans l'inégalité, autrement dit si :
mp>>m, VLo dépend nécessairement de mp. Essaie de réfléchir objectivement sans penser à ce que t'as dit ton professeur en reprenant mon message précédent : cela va te paraître évident !
PS : il y a des professeurs qui répugnent à reconnaître qu'ils ont commis une étourderie ou une faute de frappe dans leurs énoncés alors que cela peut arriver à tout le monde ! ...
Je ne peux pas t'en dire plus...

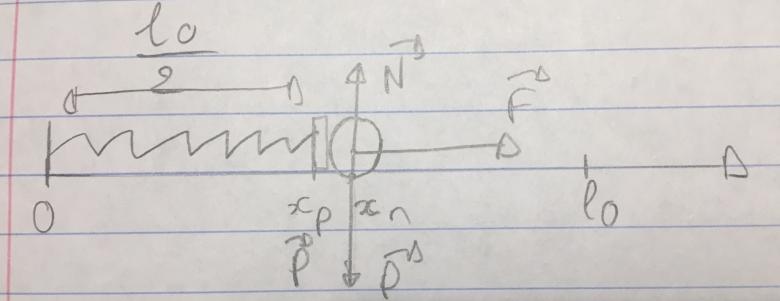

 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
