Inscription / Connexion Nouveau Sujet
Mécanique du point
Bonjour,
Je poste ce sujet car je ne sais plus la relation qu'il y a entre la réaction du support et la tension de traction. Je vous cite le sujet pour être plus compréhensible .
Un sportif remonte une luge de masse m en la faisant
glisser sur une pente inclinée d'un angle θ par rapport
à l'horizontale. Il exerce, parallèlement à la pente, une
force de traction constante, de norme , suffisante
pour mettre en mouvement la luge.
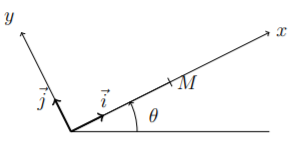
1. Faire un schéma en représentant en un point M quelconque de la pente, toutes les
forces appliquées à la luge, considérée comme un point matériel.
2. Exprimer ces forces dans la base () .
3. En utilisant le principe fondamental de la dynamique, déterminer l'expression des
composantes ax et ay de l'accélération dans la base () en fonction de m, g, k
et θ
1) J'ai fais mon schéma pas de problème
2) J'ai exprimer mes forces pas de problème
3) J'ai déterminer ax, soit ax =
Le problème est pour déterminer ay
ay =
or je dois exprimer ay en fonction de m, g,
Et je ne sais plus faire pour "transformer " en
Je sais aussi que par le calcul mais c'est tout pouvez vous m'aidez s'il vous plaît?
Bonjour
Tu n'as pas fourni de schéma. A ce que je comprends l'axe (y'y) est perpendiculaire à la trajectoire rectiligne, donc :
ay=0.
Donc si j'ai bien compris c'est que parce que l'accélération n'est faite que sur l'axe x, ay = 0 c'est cela?
Donc je n'ai pas de calcul a faire juste à expliquer c'est ça?
C'est un résultat de cours considéré comme évident au niveau post-bac mais très facile à démontrer :
Si y=0  t :
t :
vy=dy/dt=0  t
t
ay=dvy/dt=0  t
t