Inscription / Connexion Nouveau Sujet
Mecanique des solides indeformables
Bonjour!
S'il vous plait j'ai un problème sur cette exercice et j'aimerais avoir de l'aide.
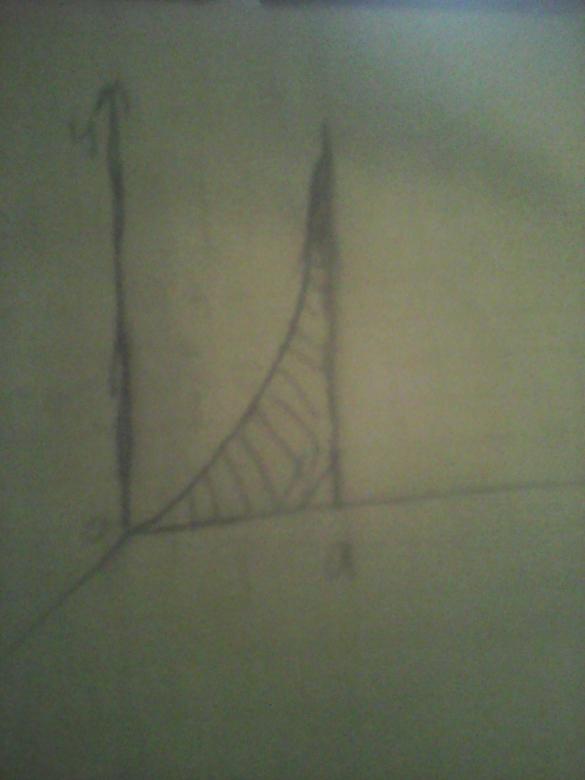
On considère la plaque homogène comprise entre la courbe y=x3, les droites y=0 , x=0 et x=a. Soit le référentiel (oxyz). La plaque se trouve dans le plan oxy. La masse surfacique est  . La plaque a un mouvement de rotation autour de son centre inertie G. On considère les axes d'inertie GX, Gy et Gz parallèle à Ox, Ou et Oz respectivement. Le mouvement de la plaque résulte de la rotation autour de Gz. Déterminer :
. La plaque a un mouvement de rotation autour de son centre inertie G. On considère les axes d'inertie GX, Gy et Gz parallèle à Ox, Ou et Oz respectivement. Le mouvement de la plaque résulte de la rotation autour de Gz. Déterminer :
1- le tenseur d'inertie de la plaque par rapport à G
2) le moment d'inertie de la plaque au point G
3) l'énergie cinétique de la plaque
Après avoir fait les calculs, obtient
Ixx=2ma6/15
Iyy=2ma2/3
Izz=2ma2(1+a4/5)/3
Ixz=Iyz=0
Ixy=ma4/4
Avec tous ces éléments je peux avoir la matrice d'inertie
Pardon dans l'expression de Izz, c'est a4 au lieu de a4 comme je l'ai écrit.
Quant au moment d'inertie j'ai appliquer la formule L=OG^mV or m= dS =
dS = dxdy
dxdy
m= a4/4kg
a4/4kg
Et G a pour coordonnées (sauf ereur)
XG=4a3/7
YG=2a3/7
ZG=0
Calculer V me derange et si je n'ai pas V je ne peux pas avoir l'énergie cinétique. Aidez moi s'il vous plait. Vérifiez aussi ce que j'ai fais à partir de la première question s'il vous plait
Bonjour
1) les formules ne sont pas homogènes!
2) quel moment d'inertie?
3) pour le solide en rotation on a ici:
Ec = 1/2  . (IG
. (IG  )
)
Bonjour krinn,
les formules ne sont pas homogènes!
J'ai eu spontanément la même réaction que toi en regardant les résultats de bissinyandoup et de JP.
Puisque "a" a la dimension d'une distance, trouver xG=4a/5 parait homogène et trouver yG=2a3/7 paraît aberrant : une ordonnée ne pouvant être homogène à un volume.
En fait : les calculs de JP me paraissent exacts (je n'ai pas vérifié tous ceux de bissinyandoup).
Le problème vient de l'énoncé lorsqu'il pose : y = x3. Pour pouvoir raisonner sur des formules homogènes, il aurait fallu poser :
y=k.x3, quitte à poser pour les applications numériques :
k=1m-2...
Alors que les programmes actuels accordent de plus en plus d'importance à l'homogénéité des formules et aux équations aux dimensions, cet énoncé est particulièrement maladroit et probablement assez ancien.
Je te laisse gérer le post.

bonsoir à tous,
je trouve aussi comme JP.
on va donc un peu oublier l'homogénéité dans cet exo, Vanoise 
C'est vrai les amis j'ai vu mon erreur. Merci pour l'attention.
Et maintenant, après avoir calculer les coordonnées de G comment fera t'on pour calculer le moment d'inertie ?
Oui krinn. J'ai pris ça dans un document.
En fait les éléments d'inertie que j'ai calculer plus haut sont ceux du centre d'inertie. Et a mon avis, pour avoir ces éléments au point O on doit appliquer le théorème de Huygens.
C'est pas exacte ??
L'idée est bonne, il y a juste un peu de confusion entre O et G à mon avis
Tu as calculé les moments d'inertie en O
Et il faut effectivement les transporter en G (centre d'inertie)
pour la 2) je pense alors qu ils demandent le moment d inertie par rapport au point G
Donc
IG = 1/2 (IGx + IGy + IGz)
je vois pas trop l'intérêt mais bon...
Ou alors ils veulent le moment cinétique par rapport à G et ce serait bien plus cohérent avec la 3e question
Si Vanoise passe ce soir, il nous dira peut être ce qu'il pense de cette 2e question 😀
Pour la 3) comme je l'ai dit ce matin
tu écris dans R* confondu ici avec Ro
Ec = 1/2  . (IG
. (IG  )
)
IG étant la matrice d'inertie en G
Avec  =
= 

Ce qui donne Ec =1/2 IGz  2
2
Bonsoir krinn, Bonsoir bissinyandoup,
Si j'ai bien compris l'énoncé : la première question demande de calculer le tenseur d'inertie en G. Pour l'instant le tenseur d'inertie de la plaque a été déterminé en O. Il faut donc, à mon avis, appliquer le théorème de Huygens généralisé sur le transport du tenseur d'inertie que j'énonce par une phrase (un peu longue), ne connaissant pas exactement les conventions de notations de bissinyandoup :
Le tenseur d'inertie de la plaque en O, que je note [IO], est la somme de deux tenseurs :
1° : le tenseur d'inertie de la plaque en G : [IG]
2° : le tenseur d'inertie en G d'une masse ponctuelle fictive égale à la masse totale de la plaque, supposée placée en G.
Pour les moments d'inertie, cela est équivalent au théorème de Huygens classique mais il faut aussi s'intéresser aux produits d'inertie...
Pour la question 2) : plutôt d'accord avec krinn : la logique voudrait que l'on demande d'exprimer le vecteur moment cinétique en G dans le repère de définition du mouvement de rotation autour de G, rotation caractérisée par le vecteur rotation instantanée : :
Pour la question 3) : l'énergie cinétique peut s'écrire :
Le vecteur rotation instantanée a, dans le cas général, trois composantes non nulles ; les produits d'inertie peuvent intervenir dans le résultat...
Sous réserve d'avoir bien interprété l'énoncé...
Merci pour toutes ces précisions, Vanoise
Il est clair quil faut transporter la matrice d'inertie y compris les produits d'inertie , on est d'accord
Je suis peut être un peu trop elliptique dans les interventions parfois ☺
le vecteur rotation instantané a généralement trois composantes non nul
Je relis l'énoncé :
La plaque a un mouvement de rotation autour de son centre inertie G
Il n'est pas écrit : "autour de l'axe (G,z)". Sans plus de précision, j'écrirais le vecteur rotation instantané sous la forme :
mais il est peut-être indiqué quelque part :
 x=
x= y=0.
y=0.
À toi de voir !
Moi je lis aussi
"le mouvement de la plaque résulte de la rotation autour de Gz"
Certes c'est du français approximatif
Mais je ne pense pas toutefois avoir surinterprete l'enonce


