Inscription / Connexion Nouveau Sujet
Mécanique des fluides - Fluide entre deux plaques mobiles
Bonjour à tous,
Je suis en 2ème année d'école d'ingénieur, actuellement en semestre d'échange dans une Hochschule Allemande.
J'ai un exercice de mécanique des fluides sur lequel je bute...
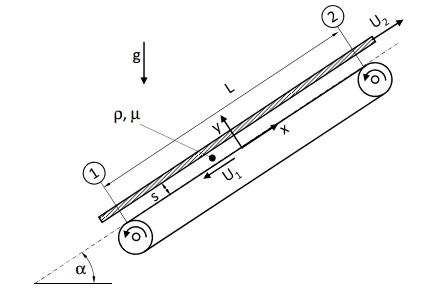
Il s'agit de l'écoulement d'un fluide Newtonien entre un tapis roulant et une plaque (voir l'image).
Énoncé:
Il existe une fente entre un tapis roulant qui se déplace à une vitesse constante vers le bas et une plaque qui se déplace à une vitesse
vers le haut.
Dans cette fente s'écoule un milieu Newtonien de masse volumique et de viscosité dynamique constante
. Ce milieu est entraîné par le tapis et la plaque, et est également sous l'influence de la force de gravitation et de la différence des pressions dans les plans
et
.
L'écoulement est stationaire, laminaire, plan et est formé sur la totalité de la longueur .
Comme , on néglige la variation de pression dans la direction
Données:
Question:
Déterminer en fonction des données la différence de pression pour laquelle la contrainte de cisaillement sur la paroi supérieure (
) est exactement égale à 0.
Aide:
Equation de Navier-Stokes dans la direction x :
Voici pour l'énoncé.
Pour l'instant j'ai réussi à déterminer la force :
J'ai également simplifié l'équation de Navier-Stoke. Comme la vitesse n'as pas de composante suivant
et
, les dérivées partielles par rapport à ces directions sont nulles. Ce qui me donne:
Et alors là je ne sais pas du tout comment continuer...
Merci à tous ceux qui pourront m'aider!
salut
j'ai du mal à te suivre sur certains trucs. Pourquoi dis-tu que la vitesse u n'a pas de composante selon x et y ? la vitesse u c'est bien la vitesse selon x, et si tu veux parler de dépendance alors tu te trompes à mon avis.
dans l'équation qu'on te donne tu peux supprimer :
- la dérivée temporelle : on est stationnaire
- les termes en v. et w.
- les dérivées par rapport à z.
par contre la dérivée selon y n'est absolument pas nulle ! justement nous on cherche du/dy à la paroi qui est la contraite de cisaillement.
il faudrait s'interroger sur la dérivée selon x : est-elle nulle ? ça nous faciliterait les choses mais étant donné le gradient de pression je pense que du/dx n'est pas nul
merci pour cette réponse rapide!
effectivement petite erreur de frappe et grosse erreur de raisonnement
Je voulais dire que la vitesse n'as pas de composante suivant
et
,
mais oui je m'étais trompé dans le raisonnement : l'écoulement est plan donc la vitesse a une composante suivant x et y.
je vais me repencher sur le problème avec la piste que tu m'as donné.
Je pense également pouvoir supprimer le terme car
je me repenche sur l'exo et vous tiens au courant,
merci encore
Et étant donné que l'on cherche la différence de pression pour laquelle la vitesse de cisaillement en y=s est nulle,
est-ce correcte de considérer
dans la mesure où une vitesse de cisaillement nulle implique du/dy = 0 et qu'on est en stationnaire, j'imagine que oui
Bonjour à tous,
le prof nous a donné des infos pour simplifier l'équation de Navier Stokes
Il s'agit d'un "ausgebildete Stroemung", littéralement "Ecoulement formé", ce qui implique le schéma ci-dessous.
Donc la vitesse ne dépend pas de
Ceci implique donc: et
On a toujours l'écoulement stationnaire qui implique (merci à Epfe, j'ai pu participer en cours en étalant ma science..!)
Concernant l'écoulement plan on peut en déduire
Comme on se place dans le cas où la contrainte de cisaillement à la paroi est nulle, on peut également dire que et
On se retrouve donc avec l'équation suivante:
Voila où j'en suis actuellement.




