Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

Mécanique des fluides

Posté par
Meedfried 09-08-21 à 17:32

Bonjour,

J'ai un exercice de Méca flu que je ne comprends pas même avec la correction.

L'embout d'une lance à incendie a un diamètre interieur D2=10cm. Il est vissé à un tube cylindrique de diamètre interieur D1=20cm. Quand l'embout est ouvert à l'air libre, la lance à incendie debite Q=40 litres d'eau par seconde. Calculer la force F a laquelle doit resister le pas de vis quand l'embout est ouvert. On negligera la pesanteur.

J'ai donc fait le théorème de la conservation quantité de masse avec F orienté vers le haut et le bas sur la surface latérale.
Voir photo
Nous somme donc en régime stationnaire avec le poids négligeable.

Pouvez vous me dire si je commence bien le problème. De plus j'ai un problème sur l'orientation de "n " dans "pnds" je ne sais pas pourquoi parfois c'est "-" parfois c'est "+". Le P c'est la pression relative ou absolue ?

Merci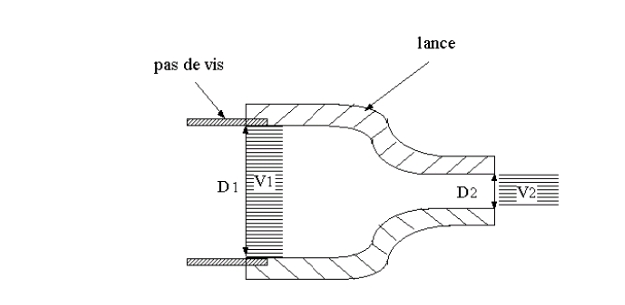

Mécanique des fluides

** image supprimée ** * mmalou > Image effacée. Merci d'utiliser les outils mis à ta disposition pour écrire les formules mathématiques *

Posté par
Meedfriedre : Mécanique des fluides 09-08-21 à 18:02

\oint_{}^{}{} rho\vec{v} ( \vec {v} . \vec{n}) ds = \oint_{}^{}{} - P \vec{n} ds

\oint_{}^{}{} rho\vec{v} ( \vec {v} . \vec{n}) ds = -rho. v1² S1 + Rho .v2² S2

\oint_{}^{}{} -P \vec{n} ds = \int -P1 .\vec{n1} dS1 + \int -Patm .\vec{n2} dS2 + \int -(P-Patm) .\vec{nlaterale} dSl

Posté par
Meedfriedre : Mécanique des fluides 09-08-21 à 18:04

Avec -F qui est égale au dernier terme de la 3eme lignes

Enfin je ne suis pas du tout sûr de moi car je ne comprends pas le vecteur normal n (normale a la surface ou au repère ex ) ...

Posté par
vanoisere : Mécanique des fluides 09-08-21 à 22:50

Bonsoir
Un simple raisonnement sur les symétries du problème permet d'obtenir la direction de la force : en effet, les composantes radiales des forces exercées par le fluide sur les parois se compensent.
Le théorème de Bernoulli ou plus simplement encore, un raisonnement sur la conservation de la masse par unité de temps permet d'obtenir les vitesses d'entrée et de sortie...
Il suffit ensuite de raisonner sur la variation en fonction du temps de la quantité de mouvement.

Posté par
Meedfriedre : Mécanique des fluides 10-08-21 à 10:08

Bonjour,
Merci

Je ne comprends pas la phrase "les composantes radiales des forces se compensent " ? Je n'arrive pas encore à me représenter la force du pas de vis correctement.

Je peux réaliser Bernoulli entre l'entrée et la sortie :
P1 + 0,5 Rho v1² - Patm - 0,5 Rho v2² = 0

Je peux aussi réaliser la conversation de la masse :
Q1= Q2
D1² V1 = D2² V2

Du coup ensuite je n'arrive pas à continuer après les équations que je vous ai mis (conservation de la quantité de masse/ mouvement )

Posté par
Meedfriedre : Mécanique des fluides 10-08-21 à 12:11

Je pense savoir ce que vous me dites, comme on a partout Patm qu'on peut prendre = 0. L'integrale d'une pression constante sur une surface fermée est nulle mais il faut prendre en compte que P1 n'est pas Patm.

Nous avons donc
\oint_{}^{}{} -P\vec{n} ds = - \int Patm. \vec{n2} dS2 +\int -Patm. \vec{nl} dSl + \int -P1. \vec{n1} dS1 + \int Patm. \vec{n1} dS1

\int -P1. \vec{n1} dS1 + \int Patm. \vec{n1} dS1 = -F

Enfin je pense pas encore avoir trouver car le résultat n'est pas bon pour F et en plus je n'utilise pas l'expression en entier...

Posté par
vanoisere : Mécanique des fluides 10-08-21 à 14:20

Les "grandes formules à rallonge" ont le mérite d'être souvent très générales et en imposent mais bon : il est bien souvent plus utile et plus rapide de réfléchir un peu. Ici, un simple raisonnement sur les symétries donne directement la direction et le sens de la force...
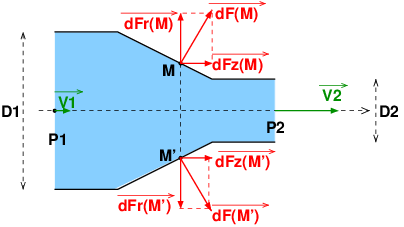
J'utilise un repère cylindro-polaire, l'axe (Oz) étant confondu avec l'axe de symétrie et orienté dans le sens de l'écoulement.
Soit un point M à la surface intérieure de la lance dans sa partie convergente ; un élément de surface dS entourant ce point et \vec n un vecteur unitaire normal à la surface et orienté vers l'extérieur. La force exercée par l'eau sur cet élément de surface vaut :

\overrightarrow{dF_{(M)}}=P_{(M)}.\overrightarrow{n}.dS
Soit M' le point symétrique de M par rapport à l'axe (Oz). On le suppose entouré d'une surface élémentaire de même aire dS, la normale étant \vec {n'}. La force exercée par l'eau sur cet élément de surface vaut :

\overrightarrow{dF_{(M')}}=P_{(M')}.\overrightarrow{n'}.dS
L'écoulement est unidirectionnel : P(M)=P(M') . Que peut-on dire de la somme vectorielle :

\overrightarrow{dF_{(M)}}+\overrightarrow{dF_{(M')}}
En généralisant ce résultat à tout couple de points {M,M'}, tu obtiens simplement la direction et le sens du vecteur force caractérisant l'action de l'eau sur la lance.
Ensuite, les aires des section droite étant connues, facile de déduire du débit les vitesses V1 et V2.
P2 étant connue, le théorème de Bernoulli te fournit la pression P1.
Enfin : un raisonnement simple sur la variation de quantité de mouvement par unité de temps permet d'obtenir la force exercée par la lance sur l'eau.
Pour conclure puisqu'il faut obtenir la force exercée par l'eau sur la lance, il suffit d'évoquer le principe des actions réciproques.

Posté par
Meedfriedre : Mécanique des fluides 10-08-21 à 19:52

Est ce que vous avez un cours ou site pour que je vois comment procéder car je suis perdu pour réaliser le qdm
Merci

Posté par
vanoisere : Mécanique des fluides 10-08-21 à 22:17

As-tu compris mon message précédent  ?
Qu'obtiens-tu comme direction et sens de la force exercée par l'eau  ?
Quel est ton raisonnement pour obtenir V1, V2, P1 et P2 ? Quelles sont les valeurs que tu obtiens  ?

Posté par
Meedfriedre : Mécanique des fluides 11-08-21 à 00:11

Merci
J'ai compris assez partiellement :
- je n'arrive pas à me dire que les forces radiales se compensent du fluide sur la paroi. Sauf pour la force exercée par l'air qui se compensent car la conduite est ouverte. L'eau a donc une action que sur l'endroit de la convergence de la lance ?
Je ne vois donc tjs pas où intervient la symétrie ...
- on peut dire de la somme vectorielle que dFm = dFm'
P dans l'expression c'est donc la pression de l'eau sur la paroi.
-Avec Q on a V1 = 1,27 m/s et V2 = 5,1 m/s
Avec Bernoulli on obtient avec P2 = Pa = 1 bar ; P1 = 1,14 bar en absolu

Posté par
Meedfriedre : Mécanique des fluides 11-08-21 à 01:27

Est ce que pour le qdm on peut pas faire un bilan des forces qui font que le système est équilibré pour trouver la force de la paroi sur l'eau ?
\sum{\vec{F}}= 0

Posté par
Meedfriedre : Mécanique des fluides 11-08-21 à 01:44

Je ne pense pas que ça marche car nous n'avons pas toutes les forces (force de maintient)

Autre idée
On peut peut être utiliser la relation \frac{d\vec{p}}{dt} = \vec{Fext}
Car ici les forces extérieures sont la force de lance sur l'eau , la force de pression du liquide en entrée et en sortie
On trouve donc par le principe des actions réciproques ce qu'on cherche ?

Posté par
vanoisere : Mécanique des fluides 11-08-21 à 15:18

Citation :
-Avec Q on a V1 = 1,27 m/s et V2 = 5,1 m/s

OK mais plutôt arrondir à 5,09m/s : il faut arrondir en donnant le même nombre de chiffres significatifs : en général trois.
Citation :
Avec Bernoulli on obtient avec P2 = Pa = 1 bar ; P1 = 1,14 bar en absolu

D'accord pour P2 mais ton résultat concernant P1 est totalement irréaliste : un fluide s'écoule de la zone à haute pression vers la zone à basse pression. Nécessairement : P1 > P2 ! Il faut toujours réfléchir au réalisme des résultats obtenus ! Je te laisse rectifier !
Citation :
je n'arrive pas à me dire que les forces radiales se compensent du fluide sur la paroi.

On s'intéresse à la résultante des forces exercées par l'eau sur les parois. On ne s'intéresse pas à l'action de l'air sur les parois extérieures. On raisonne donc en pression absolue. Observe attentivement la figure ci-dessous en reprenant mon message du  10-08-21 à 14:20. On voit bien que les composantes suivant (Oz) des deux forces s'ajoutent alors que les deux composantes radiales se compense. La force exercée par l'eau sur la lance a ainsi la direction et le sens de l'axe (Oz). On ne s'intéresse pas ici aux forces de pesanteur et à la force exercée par l'utilisateur de la lance.
Citation :
On peut peut être utiliser la relation \frac{d\vec{p}}{dt} = \vec{Fext}

Excellente idée !

Mécanique des fluides

Posté par
Meedfriedre : Mécanique des fluides 11-08-21 à 19:39

Merci bcp,

Après vérification je trouve toujours P1 = 1,13x10^5 pa donc 1,13 bar > 1 bar ... Je me posais une question, Bernoulli ici est pas plutôt faux car on prend pas en compte la perte de charge du coude ?

Du coup avec un axe x vers le haut, on a bien les composantes qui s'annulent et sur l'axe z elle s'additionnent bien.

Maintenant le qdm :
\frac{d\vec{p}}{dt} = \vec{Fext}
P= mv
donc
\frac{dm (\vec{V2}- \vec{V1})}{dt}= \vec{F lance->eau} + \int- P1 \vec{n1} dS1 + \int- Patm\vec{n2} dS2

On a la force de pression sur le coude et la force de pression du fluide en entrée et sortie.

\frac{dm (\vec{V2}- \vec{V1})}{dt}= \vec{F lance->eau} + \int P1 \vec{uz} dS1 + \int- Patm\vec{uz} dS2

D'après le principe de l'action réaction :
\frac{dm (\vec{V2}- \vec{V1})}{dt} - P1 \vec{uz} S1 + Patm\vec{uz} S2 = \vec{F lance->eau} =- \vec{F eau->lance}

Posté par
Meedfriedre : Mécanique des fluides 11-08-21 à 19:48

N'aurais je pas oublié le coefficient 2 pour la force de la lance sur l' eau ? En lien avec ce que vous avez dit ?

Posté par
Meedfriedre : Mécanique des fluides 11-08-21 à 19:57

\vec{Feau->lance} =Feau->lance.\vec{ux} -Feau->lance.\vec{ux} +Feau->lance.\vec{uz} +Feau->lance.\vec{uz} ?

Posté par
vanoisere : Mécanique des fluides 11-08-21 à 22:06

J'obtiens effectivement P1=1,13.105 Pa .
Pour la suite, tu progresses bien !
En posant Dm=.Q : débit massique, l'étude de la variation de la quantité de mouvement conduit à :

D_{m}.\left(\overrightarrow{V_{2}}-\overrightarrow{V_{1}}\right)=P_{1}\cdot\frac{\pi.D_{1}^{2}}{4}\cdot\overrightarrow{u_{z}}-P_{2}\cdot\frac{\pi.D_{2}^{2}}{4}\cdot\overrightarrow{u_{z}}+\overrightarrow{F_{lance\rightarrow eau}}

Principe des actions réciproques :

\overrightarrow{F_{eau\rightarrow lance}}=-\overrightarrow{F_{lance\rightarrow eau}}=P_{1}\cdot\frac{\pi.D_{1}^{2}}{4}\cdot\overrightarrow{u_{z}}-P_{2}\cdot\frac{\pi.D_{2}^{2}}{4}\cdot\overrightarrow{u_{z}}-D_{m}.\left(\overrightarrow{V_{2}}-\overrightarrow{V_{1}}\right)

Comme prévu qualitativement, tu vas arriver à montrer que la force exercée par la lance sur l'eau a la direction et le sens du vecteur unitaire \overrightarrow{u_{z}}.

En absence de pas de vis assurant la liaison entre le tuyau d'arrivée d'eau maintenu immobile par un pompier, l'eau entraînerait la lance dans le sens et la direction du vecteur unitaire \overrightarrow{u_{z}}. C'est donc bien cette force de vecteur \overrightarrow{F_{eau\rightarrow lance}} que l'énoncé demande d'expliciter.

Posté par
vanoisere : Mécanique des fluides 11-08-21 à 23:37

Citation :
Je me posais une question, Bernoulli ici est pas plutôt faux car on prend pas en compte la perte de charge du coude ?

En absence de précision dans l'énoncé sur la viscosité du fluide, je pense qu'il faut considérer celui-ci comme parfait (non visqueux).

Posté par
Meedfriedre : Mécanique des fluides 12-08-21 à 01:24

Merci,
Donc on a bientôt fini !

Cependant, comment peut on montrer que la force de l'eau sur la lance est uniquement sur ux ? (Il faut faire comme sur mon message de 19h57 ?)
Donc pour connaître l'action d'une force sur une paroi, il faut réaliser votre technique sur un couple de points , c'est bien ça ?

Je n'arrive pas à comprendre physiquement comment les forces radiales se compensent en fin de compte ...

Je trouve la F= 2600N

Posté par
Meedfriedre : Mécanique des fluides 12-08-21 à 12:13

Est ce qu'il serait possible de reprendre la partie 2 avec l'expression :
\oint_{}^{}{} \oint_{}^{}{}rho \vec{v} (\vec{v}.\vec{n} ) dS = \oint_{}^{}{} \oint_{}^{}{} -p\vec{n} dS

Posté par
vanoisere : Mécanique des fluides 12-08-21 à 16:36

Citation :
comment peut on montrer que la force de l'eau sur la lance est uniquement sur ux ?


J'avais noter (Oz) l'axe de symétrie mais rien n'empêche de le noter (Ox) ! On peut obtenir la direction et le sens par la méthode que j'ai exposée dans mon message du 10-08-21 à 14:20 illustrée par le schéma du 11-08-21 à 15:18. Comme la pression est la même en M et en M' (écoulement unidirectionnel) les vecteurs \overrightarrow{dF_{(M)}}=P_{(M)}.\overrightarrow{n}.dS et \overrightarrow{dF_{(M')}}=P_{(M')}.\overrightarrow{n'}.dS ont même norme. Puisque la lance admet l'axe (Oz) comme axe de symétrie, ces deux vecteurs sont inclinés par rapport à l'axe (Oz) du même angle. Les composantes radiales de ces deux forces ont même norme, même direction et des sens opposés :

\overrightarrow{dF_{r(M)}}+\overrightarrow{dF_{r(M')}}=\overrightarrow{0}

En généralisant ce résultat à tout couple de points {M,M'} on constate que la force exercée sur l'eau sur la lance n'a pas de composante radiale ; elle est donc colinéaire à (Oz). Les sens des vecteurs \overrightarrow{dF_{z(M')}} et \overrightarrow{dF_{z(M)}} montrent que cette force exercée par l'eau sur la lance est orientée dans le sens de l'écoulement.

Je trouve important ce raisonnement préalable sur les symétries du problème ; il permet souvent d'éviter de grossières erreurs. On aurait pu à la limite s'en passer. En effet, l'étude de la quantité de mouvement conduit à :

\overrightarrow{F_{eau\rightarrow lance}}=-\overrightarrow{F_{lance\rightarrow eau}}=P_{1}\cdot\frac{\pi.D_{1}^{2}}{4}\cdot\overrightarrow{u_{z}}-P_{2}\cdot\frac{\pi.D_{2}^{2}}{4}\cdot\overrightarrow{u_{z}}-D_{m}.\left(\overrightarrow{V_{2}}-\overrightarrow{V_{1}}\right)

On vérifie bien que le vecteur force est colinéaire à uz puisque les vecteurs vitesses sont colinéaires à uz..

Citation :
Je trouve la F= 2600N


En arrondissant à trois chiffres significatifs le résultat final, j'obtiens : 2,60.103N  

Posté par
Meedfriedre : Mécanique des fluides 12-08-21 à 19:48

Je vous remercie pour tout !
Pour finir, en rapport avec mon message de 12h13 ?

Posté par
vanoisere : Mécanique des fluides 12-08-21 à 22:19

Dans ce contexte, je ne comprends pas cette formule :
\oint_{}^{}{} \oint_{}^{}{}rho \vec{v} (\vec{v}.\vec{n} ) dS = \oint_{}^{}{} \oint_{}^{}{} -p\vec{n} dS
A droite : tu obtiens la résultante des forces de pression exercées sur un volume fermé a priori. Terme de droite ?

Posté par
Meedfriedre : Mécanique des fluides 13-08-21 à 12:22

Je n'ai pas vraiment plus d'informations mais je sais qu'en cours on utilisait cette formule (pour les exos de type celui ci) avec le fait qu' une même pression sur une surface fermée est nulle.

Je vous ai mis la formule complète en photo

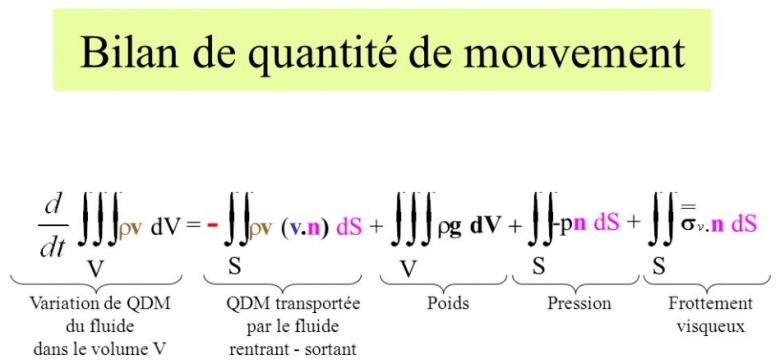
Mécanique des fluides

Posté par
Meedfriedre : Mécanique des fluides 13-08-21 à 12:24

Ce bilan de quantité de mouvement est aussi sur wikipédia
Mais du coup je ne comprends pas le terme de la pression ...

Posté par
vanoisere : Mécanique des fluides 13-08-21 à 14:36

Citation :
Mais du coup je ne comprends pas le terme de la pression ...

Soit un point M appartenant à la surface fermée délimitant le volume de contrôle sur lequel tu effectues ton bilan. Soit une surface élémentaire d'aire dS entourant le point M et le vecteur unitaire normal \vec n orienté vers l'extérieur du volume de contrôle.
Le fluide exerce sur la surface élémentaire la force élémentaire ;

\overrightarrow{dF_{(M)}}=P_{(M)}.\overrightarrow{n}.dS \\
Principe des actions réciproques, le milieu extérieur exerce la force élémentaire :

\overrightarrow{dF}=-P_{(M)}.\overrightarrow{n}.dS \\
Si la surface de contrôle en M est une parois rigide, \overrightarrow{dF} est une force élémentaire exercée par l'élément de paroi d'aire dS. Si la surface de contrôle en M appartient au fluide, \overrightarrow{dF} est une force élémentaire exercée par le fluide extérieur, celui situé en amont ou en aval de celui présent à l'intérieur du volume de contrôle.

Posté par
Meedfriedre : Mécanique des fluides 13-08-21 à 16:19

D'accord,

Si on raisonne comme sur :
"http://hmf.enseeiht.fr/travaux/CD0102/travaux/2h/tpld/moulins/sommaire/theorie/jetplat.htm" ou le pdf en pièce jointe.
pdf
PDF - 477 Ko

On a :

Meedfried @ 09-08-2021 à 18:02

\oint_{}^{}{} rho\vec{v} ( \vec {v} . \vec{n}) ds = \oint_{}^{}{} - P \vec{n} ds

\oint_{}^{}{} rho\vec{v} ( \vec {v} . \vec{n}) ds = -rho. v1² S1 + Rho .v2² S2 =152.8 N

Sur l'autre terme, nous avons la pression atm sur S1 et S2 (force exercée par le fluide ) et la différence entre la pression interne et atm sur la surface latérale ? et avec ca on trouve F ?


Je suis désolé si je vous demande beaucoup ...

Posté par
vanoisere : Mécanique des fluides 13-08-21 à 17:02

Je raisonne sur le volume de contrôle en bleu sur mon schéma précédent :
1° : Le terme de pression \\ \oint_{}^{}{} - P \vec{n} ds est une somme de trois termes :
La force exercée par l'eau sur la lance : \overrightarrow{F_{eau\rightarrow lance}} ;
2° : la force de pression exercée par l'eau en amont :

P_{1}\cdot\frac{\pi.D_{1}^{2}}{4}\cdot\overrightarrow{u_{z}}
3° : la force de pression exercée par l'eau en aval :

-P_{2}\cdot\frac{\pi.D_{2}^{2}}{4}\cdot\overrightarrow{u_{z}}
Analysons maintenant le terme :

\\ \oint_{}^{}{} \rho\vec{v} ( \vec {v} . \vec{n}) ds

\rho.\overrightarrow{v}.\overrightarrow{n}.dS représente le débit massique à travers la surface élémentaire d'aire dS. Ce débit étant considéré comme positif pour les flux sortant et négatif pour les flux entrant. Pour les surfaces imperméables au fluide, le débit est nul car les vecteurs \vec v et \vec n sont orthogonaux. En multipliant ce produit scalaire par \vec v tu obtiens la quantité de mouvement élémentaire traversant la surface élémentaire. Dans le cas particulier de notre étude, cela donne :

\oint \rho.\vec{v}(\vec{v}.\vec{n})dS=D_{m}.\left(\overrightarrow{V_{2}}-\overrightarrow{V_{1}}\right)
Cela conduit heureusement au résultat déjà obtenu.
Je me permets de recopier ma première phrase concernant cet exercice :
Les "grandes formules à rallonge" ont le mérite d'être souvent très générales et en imposent mais bon : il est bien souvent plus utile et plus rapide de réfléchir un peu. Ici, un simple raisonnement sur les symétries donne directement la direction et le sens de la force...

Posté par
Meedfriedre : Mécanique des fluides 13-08-21 à 17:32

Merci beaucoup, je vois donc le rapprochement.

Je fais également le rapprochement des 2 exos.
En force de pression on pourrait aussi rajouter la pression de l'air sur la conduite.
En effet on trouve F = 2,6*10^3 N suivant uz mais elle se compense aussi par la force de l'air sur la conduite.

Sur la surface D1, j'ai pas mis de flèche car la surface n'est pas à l'air libre donc pas de pression Patm
Donc \vec{F} = -Patm *\vec{uz}* S2
Donc F = 785 N suivant -uz ?

Mécanique des fluides

Posté par
vanoisere : Mécanique des fluides 13-08-21 à 18:18

En notant S2 et S1 les aires des disques de diamètres D2 et D1, on obtient directement par raison de symétrie et en utilisant le raisonnement donné dans l'autre exercice :

\overrightarrow{F_{air\rightarrow lance}}=-P_{atm}\cdot\left(S_{1}-S_{2}\right)\cdot\overrightarrow{u_{z}}

Cette formule  pourrait éventuellement être affinée en tenant compte de l'épaisseur du métal constituant la lance mais elle constitue je pense une excellente approximation.

Posté par
Meedfriedre : Mécanique des fluides 14-08-21 à 16:37

Encore merci !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !