Bonjour, d'accord merci j'ai compris
par contre pour mon premier problème j'insiste encore un petit peu si cel ane vous dérange pas

Je me permet de mettre un autre exemple :

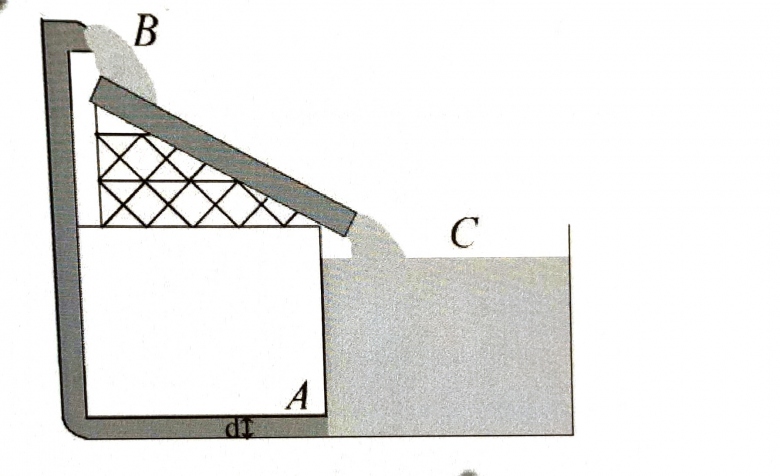
On considère une piscine toboggan ouvert à l'air libre, dans un parc d'attraction. Une conduite d'aspiration de diamètre d=15cm permet d'aspirer au point A l'eau de la piscine à un débit volumique Q de 10,6L/s afin de l'acheminer jusqu'au sommet du toboggan comme représentée sur la figure ci-dessous. On suppose que l'eau, assimilée à un fluide non visqeux, est en circuit fermé et que le niveau de la piscine reste constant .

On donne :
-la différence de hauteur entre les points A et B = 7,3m
-la différence de hauteur entre le point A et C =  2m

Quelle est la pression au point A ?

Là je ne comprends pas pourquoi on ne peut pas utiliser le principe de la statistique des fluides pgh ici, car j'ai dit que le point A a la même pression au point A' qui est a l'interface du bassin et du tuyau en bas , et donc finalement appliquer le principe.
Mais au final il fallait utiliser le theroème de bernoulli
Donc je ne comprends dans quel cas applique t on le principe pgh ? Merci



*** message déplacé ***

Bonjour,

P(A) est bien égal à P(A') comme précédemment. Mais ici entre A et C, c'est assez compliqué : l'eau s'écoule depuis la surface en convergeant vers l'entrée du tuyau, donc la vitesse varie beaucoup entre la surface (quasi) et l'entrée (vitesse nécessaire au débit). Il n'y avait pas d'eau qui s'écoulait dans le petit tube.
Sinon dans le grand tuyau précédent, vous pouvez appliquer Bernoulli en utilisant la totalité des hypothèses (parfait, permanent, irrotationnel) entre la sortie du petit tuyau et le point B ; l'altitude est constante, la vitesse aussi, donc P constante. Et cela est relativement général : pour un champ de vitesse parallèle, le champ de pression est hydrostatique pour un fluide parfait.

*** message déplacé ***

Ah d'accord donc si j'ai bien compris, c'est un problème de vitesse .

Mais je bloque toujours sur la question : est ce que j'ai le droit d'utiliser le principe pgh. Car à l'exercice précedent, la vitesse au point B était inconnue donc elle aurait pu être très grande par rapport au petit tube et finalement on aurait pas pu négliger celle ci comme dans cet exercice ci dessus ?

Finalement, on utilise pgh dans la mesure où on a deux fluides immobiles ou 1 seul immobile et 1 autre dont la vitesse est assez faible ? si je comprends bien
Merci beaucoup

Bonjour,

On utilise la loi de l'hydrostatique pour un fluide au repos.

Dans l'exercice avec le gros tuyau vertical et les prises de pression latérales, on utilise en fait trois choses :
- hydrostatique dans le petit tube
- continuité de la pression
- isobare horizontale dans l'écoulement parallèle ( vitesse grande ou non, on ne néglige rien).

Dans le cas au-dessus on néglige la vitesse en C par rapport à celle en A et on applique Bernoulli. Il n'y a aucune zone hydrostatique dans le schéma ci-dessus dans lequel on pourait appliquer le principe de l'hydrostatique, ce qui n'était pas le cas dans l'autre (petits tubes au repos).

Ah okay je comprends beaucoup mieux dit comme ceci Merci beaucoup

Par contre, quand vous dites isobare horizontale pour l'exercice précedent, j'étais persuadé également que cela ne s'appliquait qu'à un fluide immobile ? ou est ce que cest la meme raison énoncée dans votre message ?

Oui, en effet :

1- champ de vitesse parallèle, fluide parfait, donc la pression suit la loi de l'hydrostatique et en particulier P=Cte sur une horizontale

ou

2- écoulement uniforme irrotationnel, donc Bernoulli en tout point ce qui conduit à la même chose.

Je ne comprends pas tout désolé
Comment sait on que dans l'exercice avec le gros tuyau on avait un champ de vitesse parallèle sachant que le tuyau comporte une vitesse nulle ?Merci

L'énoncé est en effet succinct, mais vous avez cet exo dans le cadre simple des fluides parfaits. Dans cette première approche, on fait l'hypothèse écoulement laminaire non visqueux, et il parait raisonnable de supposer que dans un conduit cylindrique, l'eau a un mouvement parallèle à la paroi.

Le "sachant que le (petit je suppose) tuyau comporte une vitesse nulle" n'a rien  à voir ici.

ah okay je comprends, je vais essayer d'appliquer tout ceci parce que je n'ai pas encore les idées claires sur les conditions d'application du principe