Inscription / Connexion Nouveau Sujet
mecanique des fluides
Bonsoir à toutes et tous,
svp si quelqu'un peu m aider ou avoir son avis ! j ai fais un calcul pour l'exercice ci-après, mais je ne suis pas sur de moi .merci
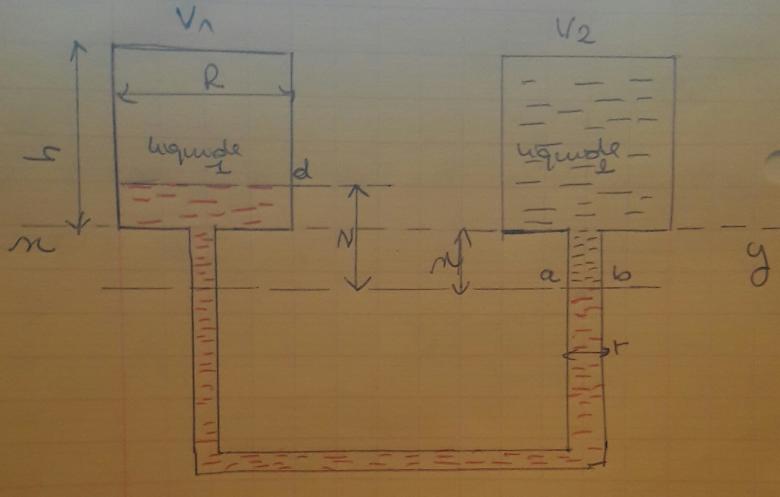
Soit deux vases cylindriques V1 et V2, de rayon R et de hauteur h , ouverts à leur partie supérieure, réunis par un tuyau cylindrique de rayon r,
Ce tube est rempli jusqu'au plan horizontal XY avec un liquide de masse volumique p.
Le vase V2 est ensuite, complètement rempli avec un liquide de masse volumique p'.
Le premier liquide est alors refoulé en ab d'un côté et en cd de l'autre .
Il est demandé d'évaluer la distance z entre ab et cd.
Application : R=1,00 m ; r=0,10 m ; h=8,000 m.
Liquide 1 : mercure
Liquide2 : eau.
Nous avons :
Le liquide 1 est un mercure de masse volumique ρ qui affleurait en XY . Pa étant la pression atmosphérique :
ϖ= ρ g = 13600 x 9.81= 1,33.105 N
P1= Pa + ρ g h1
Dans le vase V2 , Le liquide 2 : eau de masse volumique ρ' versée, Pa étant la pression atmosphérique :
ϖ= ρ g = 1000 x 9.81= 9810 N
P2 = Pa + ρ g h2
Au point ab :
Le niveau correspondant au point ab est a la même pression car il est dans le même liquide (mercure) et dans le même plan horizontal.
P1(ab) = P0 + Peau = P0 + ρgh
P2(ab) = PHg + P0 = ρ'gh' + P0
d'où :
ρgh = ρ'gh'
ρh = ρ'h'
h' = ρ h/ρ' = ( 1000x 8 )/13600 =0.59 m
La distance z entre ab et cd = 0.59 m
Bonjour ,
Combien vaut , d'après vos calculs , la distance entre le plan ab et le fond des vases xy ?
il y a une flèche montrant cette cote qui est notée n ou x , je n'arrive pas à lire exactement .
Bonjour quarkplus, merci pour la réponse.....
(la distance entre le plan ab et le fond des vases XY notée x)
d'abord je dois rectifier:
ρgz = ρ'g (h+x )
ρz = ρ' (h+x)
Bonjour quarkplus, merci pour la réponse.....
(la distance entre le plan ab et le fond des vases XY notée x)
d'abord je dois rectifier:
ρgz = ρ'g (h+x )
ρz = ρ' (h+x)
C'est déjà beaucoup mieux.
Il te manque encore une équation reliant x et z pour pouvoir calculer ces 2 grandeurs ...
Réfléchis sur les volumes ...
Le volume de liquide 1 qui a été évacué de la partie du tube à droite sur le dessin a été transféré dans le cylindre V1 et donc ...
Attention que sur ton dessin, il y a confusion entres Rayons et diamètres.
Sauf distraction.

merci quarkplus ..merci J-P ( désolée pour le retard j'attendais ma pause déjeuner pour répondre )
)
équation reliant x et z :
z= (x+h)(1/13.6)
Le volume de liquide 1 qui a été évacué de la partie du tube à droite sur le dessin a été transféré dans le cylindre V1 donc :
Volume liquide 1 évacué de la partie du tube = Volume liquide 1 transféré dans le cylindre
nous avons aussi le volume de liquide 2 versé dans le cylindre V2 = PiR²h=25.12m^3
Volume évacué du tube : V3 = Pi.r².x
Volume rejeté dans le cylindre V2 : V4 = Pi.R².(z-x)
V3 = V4 --> Pi.r².x = Pi.R².(z-x)
r².x = R².(z-x)
-----
On a donc le système d'équations d'inconnues x et z :
r².x = R².(z-x)
Rho.z = Rho'.(h+x)
Qu'il suffit de résoudre ...
Sauf distraction. 
merci beaucoup J-P...
donc (rapidement)
r².x = R².(z-x)
Rho.z = Rho'.(h+x)
0,01 . x=z-x
13600. z = 1000(8+x)
0,01 . x+x=z
13600(0,01x .+ x) = 8000+1000x
136x+13600x-1000x =8000
x=8000/12736= 0,63m
0,01 . 0,63+0,63=z
z= 0,64m
Z plus grand que x ? Impossible ...
D'où proviendrait le cm de mercure répandu au fond de la cuve V1 ?
De plus : 0.64 13600 = 8704 différent de 8.63 1000 = 8630 .
"Z plus grand que x ? Impossible ... "
Bien sûr que si.
J'ai bien l'impression que tu n'as pas capté où Z a été choisi.
Le Z est en fait ce que tu penses être N sur le dessin...
Mais c'est un Z écrit dans le sens vertical sur le dessin.
On a donc obligatoirement Z > x (voir sur le dessin)
On trouve z = 0,6281 m et x = 0,6219 m
... à arrondir en fonction du nombre de chiffres significatifs adéquats.
La distance entre les niveaux ab et cd est z.

mon erreur était de dire , le niveau de mercure ne monte pas ... OK , c'est vu .
Donc , les résultats de nano seraient trop arrondis ...
Maintenant vos résultats , la preuve ne marche pas ?
13600 . 0.6281 = 8542 et
1000 . 8.6219 = 8622 Pourquoi ?
Mes résultats z = 0.6357 et x = 0.6457
13600 . 0.6357 = 8646
1000 . 8.6457 = 8646
Bonjour odbugt ,
Donc la preuve pour vos résultats :
0.63442211 . 13600 = 8628.14
8.628140703 . 1000 = 8628.14
C'est bon pour vous !
Mais pour moi aussi ! Comment se fait il plusieurs jeux de résultats , mes 2 valeurs sont bien indépendantes , je n'ai pas déduit l'une de l'autre ....
Bien , j'ai forcément une erreur , j'ai Z plus petit que x !!!
Par contre la preuve marche , là je ne comprends plus , j'abandonne ...
Conformement à mon message du 14-08-17 à 16:13
r².x = R².(z-x)
Rho.z = Rho'.(h+x)
0,01.x = 1*(z-x) ---> z = 1,01.x --> x = z/1,01
13600.z = 1000 * (8+x) --> 13,6z = 8 + x
13,6z = 8 + z/1,01
z = 8/(13,6 - 1/1,01)
z = 0,6344 m (qui est la distance demandée par l'énoncé)
Et pas demandé : x = 0,6344/1,01 = 0,6281 m
A arrondir ...

Bonjour,
Je pense que, vu le très petit écart relatif entre les valeurs de z et de x ( de l'ordre de 1%) votre preuve doit être mise en œuvre avec un plus grand nombre de chiffres significatifs.
C'est la raison pour laquelle j'en ai mis bien trop pour rendre un résultat, mais suffisamment pour que votre preuve soit efficace.


