Inscription / Connexion Nouveau Sujet
Mécanique des fluides
Bonjour,
J'aurais besoin de votre aide pour résoudre l'exercice suivant s'il vous plaît. Merci d'avance ! 
_______________________________________________________________________________________________________
I. Modèle météorologique
Un point situé dans l'atmosphère est repéré par ses coordonnées
dans le repère terrestre local
dont l'origine
se trouve dans un plan méridien à la latitude
(figure N°1) avec
pour l'hémisphère Nord, l'axe
étant dirigé vers l'Est, l'axe
étant dirigé vers le Nord et l'axe
étant dirigé suivant la verticale ascendante.
On prendre .
1. On s'intéresse à la résultante des forces de pression s'exerçant sur un élément de fluide atmosphérique de masse
, de forme parallélépipédique, de volume
.
Montrer que la force de pression rapportée à l'unité de masse, définie par est donnée par l'expression
où
est la masse volumique du fluide en
et
la pression en
(figure N°2).
Dans une atmosphère calme, par quoi est compensée la composante verticale des forces de pression ?
Par la suite, on supposera cette compensation effective en toutes circonstances et on ne s'intéressera qu'au mouvement de la particule de fluide dans un plan horizontal.
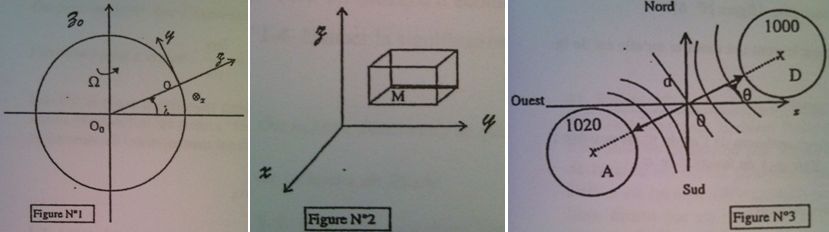
2. Soit la situation météorologique schématisée sur la figure N°3 dans laquelle l'axe anticyclone-dépression fait un angle avec la direction
. La distance entre les isobares 1020 et 1000 est notée
, les pressions étant mesurées en hectopascals. On supposera le gradient de pression uniforme sur l'axe
, sa norme étant notée
.
N.B. : Au niveau de l'axe les isobares sont perpendiculaires à cet axe et sont localement assimilables à des segments de droite.
Exprimer les composantes et
de la forme massique de pression en fonction de
.
_______________________________________________________________________________________________________
1. On a , d'où
.
Dans une atmosphère calme, la composante verticale des forces de pression est compensée par le poids, non ?
2. Je n'ai pas vraiment compris la question...
Attention c'est un météorologue qui te parle 
Tu es d'accord que tu as un gradient de pression entre A et D ?
Tu as donc une force de pression qui si on néglige la force de Coriolis va pousser les particules d'air de l'anticyclone vers la dépression.
Il faut juste que tu exprime cette force de pression massique en fonction des données du problème.
Attention c'est un météorologue qui te parle
Ça tombe bien !

Tu es d'accord que tu as un gradient de pression entre A et D ?
Tout à fait.
Tu as donc une force de pression qui si on néglige la force de Coriolis va pousser les particules d'air de l'anticyclone vers la dépression.
Il faut juste que tu exprime cette force de pression massique en fonction des données du problème.
Je ne vois pas trop... Est-qu'on aurait
Tu as démontré à la question précédente l'expression de la force par unité de masse de pression avec un facteur égal à l'inverse de la masse volumique. Je ne vois pas pourquoi tu fais passer la masse volumique d'un coup au numérateur, du coup elle ne te parait homogène à juste titre.
donc fx=(1/rho).a.cos(theta) et fx=(1/rho).a.sin(theta)
C'est une faute de frappe... La masse volumique est, bien évidemment, au dénominateur.
Mon problème d'homogénéité venait du fait que je croyais que était homogène à une longueur, sauf que j'avais tord : c'est la norme du gradient de pression, donc c'est bien homogène à une pression divisé par une longueur

Voilà la suite :
_______________________________________________________________________________________________________
3. Le référentiel géocentrique étant supposé galiléen, on se place dans un référentiel terrestre. Quelles sont les forces qui agissent sur une particule de fluide. Qu'appelle-t-on poids de la particule ?
Écrire le P.F.D. pour la particule de fluide dans le référentielle terrestre.
4. Projeter l'équation sur les axes et
et montrer qu'en régime de "vitesse constante", le fluide atmosphérique s'écoule au niveau de l'axe
suivant une direction et un sens que l'on précisera avec soin sur la figure N°3.
Comment modifier ces conclusions dans l'hémisphère Sud ?
5. Cherche la norme du vecteur vitesse du vent. Calculer sa valeur numérique (.
_______________________________________________________________________________________________________
3. Les forces exercées sur le système sont le poids et la force de pression. Pourquoi est-ce qu'on nous demande ce qu'on appelle poids de la particule ? Je ne vois pas quelle réponse est attendue...
Le P.F.D. s'écrit : .
4. En projection sur .
En projection sur .
Est-ce correct ?
Non c'est faux.
Le référentiel géocentrique étant supposé galiléen, on se place dans un référentiel terrestre.
Ce référentiel terrestre (0,x,y,z) est t'il galiléen ?
Conséquences ?
En effet, il faut donc rajouter les forces d'inertie d'entraînement et de Coriolis.
Le P.F.D. fournit donc : 3$ \vec{a}=-\frac{1}{\rho}\vec{grad}P+\vec{g}+\Omega^2\vec{HM}-2\vec{\Omega} \wedge \vec{v_r} où 3$ H est le projecteur orthogonal de 3$ M sur l'axe de rotation et 3$ \vec{v_r} la vitesse relative.
Est-ce correct cette fois ? Mais que vaut la vitesse relative ? ...
Pour le poids en fait on considère en mécanique terrestre que c'est la somme de g et force d'inertie d'entrainement terrestre...lis ton cours ça devrait être détaillé.
C'est ce qui explique la différence des valeurs de gravité qu'on donne aux poles ou à l'équateur.
Pour la vitesse relative ben c'est la vitesse dans le référentiel non galiléen dx/dt + dy/dt
Essayes de projeter ça.
bonus physique parce que j'aurai plus le temps de poster ajd.
En première approximation les particules se déplacent en ligne droite de l'anticyclone vers la depression (ca te donne une certaine vitesse).
Regardes la direction de la force de coriolis dans ce cas. tu verra que les particules vont s'enrouler dans le sens trigo autour d'une dépression et le sens horaire autour d'une dépression. Ces conclusions sont valables dans l'émisphère nord.
Dans l'émisphère sud si tu veux conserver tes axes x y en sud nord et ouest est il va falloir prendre l'opposé au niveau du vecteur qui complète ta base et donc un vecteur rotation opposé.
Donc ca change complètement les sens d'enroulement dans l'Emisphère sud.
On a fait le tour de la physique du problème à ce niveau.


