Niveau maths sup

Mécanique (coordonnées polaires)

Posté par
Marie314 26-08-22 à 17:18

Bonjour à tous,
Pour la rentrée, j'ai un DM de physique à faire, et je bloque sur certaines questions. En voici une, avec l'énoncé :

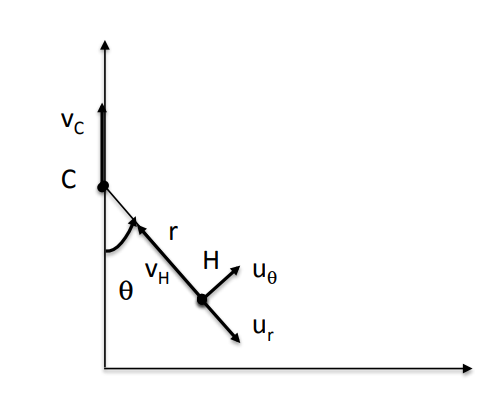
Calvin - noté C - se meut à vitesse constante vC sur une droite confondue avec l'axe y. Son tigre Hobbes, H, qui lui est initialement distant de r0 dans la direction perpendiculaire à cette droite, court vers lui à la vitesse de norme vH constante. On cherche une condition pour que Hobbes puisse rattraper Calvin. Pour cela, on décrit le mouvement relatif de Hobbes par rapport à Calvin, on repère ainsi la position de H rapport à C en coordonnées polaires (r, thétâ), plus précisément, on note r la distance entre Calvin et Hobbes et thétâ l'angle entre la direction de Hobbes et celle opposée au vecteur vC .

18 - Exprimer le vecteur v C dans la base polaires (ur, u(thétâ)) en fonction de vC et thétâ. Exprimer de même la vitesse de Hobbes : vecteur vH, dans la base polaire.

Je n'ai jamais manié des coordonnées polaires en terminale (j'ai conscience qu'il s'agit d'une lacune qu'il me faudra combler), donc je ne sais pas vraiment quoi faire... J'ai essayé deux approches différentes : exprimer vC avec ur et u(thétâ) de telle sorte que :

vC(en vecteur) a pour coordonnées : (-cos(thétâ)vc ; sin(thétâ)vc).

Et pour vH, j'ai essayé de dériver le vecteur position par rapport au temps, mais comme C est un point en mouvement je n'ai pas su si je pouvais...
Bref, je ne sais pas quoi faire. Si quelqu'un pouvait m'aider, je lui en serai vraiment reconnaissante!!

Mécanique (coordonnées polaires)

Posté par re : Mécanique (coordonnées polaires) 26-08-22 à 17:48

Bonjour
Voici un document sur les coordonnées polaires. A toi d'adapter mais le résultat fourni te donne immédiatement le résultat de la vitesse de H dans le repère mobile (C,x,y).
PS : ce problème me fait penser au problème de poursuite sur le chien d'Euler ...

Posté par re : Mécanique (coordonnées polaires) 27-08-22 à 12:10

Merci, effectivement c'est bien expliqué!
J'ai aussi été voir le problème du chien d'Euler, qui ressemble assez à ce problème. Malheureusement je ne comprends toujours pas comment exprimer vC dans la base polaire, surtout si C est le point sur lequel se centre le référentiel... Comment exprimer un vecteur position dans ce cas, pour le dériver ensuite et trouver la vitesse vC? Je ne comprends pas ce point...

Posté par re : Mécanique (coordonnées polaires) 27-08-22 à 17:57

Ton énoncé n'est pas très précis et, sans le connaître en entier, difficile de te conseiller très efficacement... A ce que je comprends, $\overrightarrow{V_{C}}$ désigne le vecteur vitesse du point C dans le repère absolu (O,x,y) mais il est cependant tout à fait possible de l'exprimer dans la base polaire mobile :

$\overrightarrow{V_{C}}=V_{C}.\overrightarrow{u_{y}}=-V_{C}.\cos\left(\theta\right).\overrightarrow{u_{r}}+V_{C}.\sin\left(\theta\right).\overrightarrow{u_{\theta}}$

La vitesse absolue de H, c'est à dire la vitesse de H par rapport au repère (O,x,y) est la somme de deux vecteurs :

1° : la vitesse d'entraînement qui est ici la vitesse de translation du repère (C,x,y) par rapport au repère (O,x,y) : $\overrightarrow{V_{C}}$

2° : la vitesse relative qui est la vitesse de H dans le repère (C,x,y) : la vitesse fournie dans le document que je t'ai fourni :
Dans le repère absolu (O,x,y) :

$\overrightarrow{V_{H}}=\overrightarrow{V_{C}}+\dot{r.}\overrightarrow{u_{r}}+r.\dot{\theta}.\overrightarrow{u_{\theta}}=\left(\dot{r}-V_{C}.\cos\left(\theta\right)\right).\overrightarrow{u_{r}}+\left(r.\dot{\theta}+V_{C}.\sin\left(\theta\right)\right).\overrightarrow{u_{\theta}}$

Posté par re : Mécanique (coordonnées polaires) 27-08-22 à 19:01

Merci pour ton aide, de nouveau!

Concernant $\vec{vC}\$ , j'ai trouvé la même chose que toi, ça me rassure. En revanche, concernant $\vec{vH}\$ , j'ai uniquement mis : $vH.\vec{ur} + r\dot{\theta }.\vec{u_{\theta }}$ . Je comprends qu'il faut rajouter $\vec{vC}\$ pour exprimer $\vec{vH}\$ dans la base (O,x,y), mais dans la base polaire, faut-il le mettre aussi?

En fait, une base polaire, c'est juste la donnée de deux vecteurs formant une base orthonormée, avec pour origine un point en mouvement (ici H). C'est bien cela (histoire d'être sûre de comprendre)?

De plus, la question précise qu'il faut exprimer $\vec{vC}\$ en fonction de $\theta$ et de $vC$ . Et de faire de même avec $\vec{vH}\$ . Est-ce donc bon de remplacer $\dot{r}$ par vH (comme je l'ai fait) et aussi de remplacer $r$ par $\int vH$ ?

D'autant plus que mon énoncé précise :

"On donne $\int \frac{\partial x }{ sinx} = ln(tan\frac{x}{2})$ et $\int \frac{\partial x}{tan x} = ln(sinx)$ ".

Mais je pense qu'il s'agit d'indications pour la question suivante, qui est :

"On admet que dans le référentiel R' lié à Calvin, la vitesse $\vec{v'H}$ du tigre est donnée par $\vec{v'H}=\vec{vH}-\vec{vC}$ . On écrit cette vitesse en coordonnées polaires.
* Rappeler l'expression générique de la vitesse $\vec{v'H}$ en polaires [je pense donc qu'il s'agit de la valeur que j'avais trouvée initialement pour vH, et qu'il faut effectivement rajouter, pour la question précédente, le vecteur vC comme tu me l'as conseillé].
**En utilisant la relation $\vec{v'H}=\vec{vH}-\vec{vC}$ et les expressions polaires de $\vec{vH}$ et $\vec{vC}$ fournies précédemment, exprimer $\vec{v'H}$ dans la base polaire en fonction de vC, vH et $\theta$ [je ne comprends pas en quoi les deux questions, * et **, sont différentes].

Voilà, tu as tout mon énoncé, le but étant de trouver les conditions pour lesquelles Hobbes rattrape Calvin...

Posté par re : Mécanique (coordonnées polaires) 27-08-22 à 23:38

N'ayant pas tout l'énoncé lors de mon message précédent, je pense avoir utilisé des notations non conforme à celles demandées.
Maintenant que tu as copié de larges extraits de l'énoncé, le règlement du forum t'autorise à poster ici l'énoncé intégral sous forme de fichier pdf (cliquer sur l'icône Pdf en bas de cet éditeur) ou éventuellement sous forme d'image jpg (cliquer sur l'icône Img).

Posté par re : Mécanique (coordonnées polaires) 28-08-22 à 09:07

Alors voilà :

Mécanique (coordonnées polaires)

Posté par re : Mécanique (coordonnées polaires) 28-08-22 à 10:51

Merci pour l'énoncé. La situation est plus claire : on note R le repère absolu lié à la terre (O,x,y) et on note R' le repère relatif en translation par rapport à R à la vitesse $\overrightarrow{V_{C}}$ , c'est à dire le repère (C,x,y). Les vitesses absolues de C et de H, donc les vitesses par rapport à R, exprimées dans la base polaires sont :

$\overrightarrow{V_{C}}=V_{C}.\overrightarrow{u_{y}}=-V_{C}.\cos\left(\theta\right).\overrightarrow{u_{r}}+V_{C}.\sin\left(\theta\right).\overrightarrow{u_{\theta}} \\ \\ \overrightarrow{V_{H}}=-V_{H}.\overrightarrow{u_{r}}$

Comme expliqué dans mon message du 27-08-22 à 17:57 mais avec des notation non adaptées, faute d'énoncé complet, la vitesse relative de H, c'est à dire sa vitesse dans R', est la différence entre la vitesse absolue et la vitesse d'entraînement :

$\overrightarrow{V'_{H}}=\overrightarrow{V_{H}}-\overrightarrow{V_{C}}=\left[V_{C}.\cos\left(\theta\right)-V_{H}\right].\overrightarrow{u_{r}}-V_{C}.\sin\left(\theta\right).\overrightarrow{u_{\theta}}$

Or, l'expression “générique” de la vitesse dans R' est (voir document fourni) :

$\overrightarrow{V'_{H}}=\dot{r}.\overrightarrow{u_{r}}+r.\dot{\theta}.\overrightarrow{u_{\theta}}$

Il est alors possible d'identifier :

$\dot{r}=V_{C}.\cos\left(\theta\right)-V_{H}\quad;\quad r.\dot{\theta}=-V_{C}.\sin\left(\theta\right)$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Mécanique (coordonnées polaires)

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique