Niveau maths spé

Mécanique 9

Posté par
Flewer47 02-08-16 à 16:00

Bonjour,

Je n'arrive pas à trouver la réponse à la dernière question de cet exercice, dont voici l'énoncé :
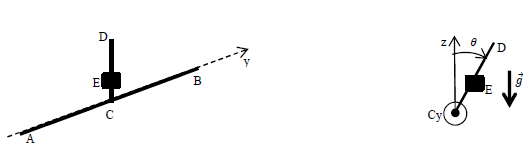
Pour mesurer les variations de g, on utilise le dispositif suivant : une tige mince, homogène, verticale $CD$ de longueur $h=10 cm$ , de masse $m=20 g$ ,de moment d'inertie $J=\frac{mh^2}{3}$ par rapport à un axe $Cz$ , est fixée rigidement au milieu d'un fil de torsion $AB$ de longueur $L=50 cm$ horizontal. Sur la tige peut coulisser une masselotte $E$ de masse $M=50 g$ . Le fil $AB$ est un fil de torsion en acier de constante de torsion $K=4.10^{-2} N.m.rad^{-1}$ .
1) Calculer en fonction de $x=CE$ la période des petites oscillations de la tige autour de la position verticale ascendante. Quelle est la limite $x_0$ à ne pas dépasser ? Que se passe-t-il si $x>x_0$ ? On suppose que $g=9,8 m.s^{-2}$ .
2) On fixe la masselotte dans une position $x_1$ de telle sorte que la période soit $T=10s$ pour $g=g_0$ . Calculer $x_1$ . On suppose maintenant que l'appareil est transporté en un autre lieu, quelle variation relative $\frac{\Delta g}{g_0}$ correspond à une variation de période $\frac{\Delta T}{T_1}=10^{-3}$ .

Voici ce que j'ai trouvé :
1) $T=2\pi \sqrt{\frac{\frac{mh^2}{3}+Mx^2}{K-g(Mx+\frac{mh}{2})}}$ .
$x_0=\frac{K}{Mg}-\frac{mh}{2M}$ . Si $x>x_0$ , le mouvement n'est plus sinusoïdal et est non borné.
2) $x_1=\frac{-\frac{25gM}{\pi ^2}+\sqrt{\frac{625g^2M^2}{\pi ^4}-4M(\frac{mh^2}{3}-\frac{25K}{\pi ^2}+\frac{25gmh}{2\pi ^2})}}{2M}=0,06142 m$ .

La dernière question me fait penser à la dérivée de Ln, mais je ne vois pas comment y arriver, car je ne vois pas comment avoir $Ln(T)=f(g)$ (avec $f$ une fonction..)

Merci de votre aide !

Mécanique 9

Posté par re : Mécanique 9 02-08-16 à 19:49

A mon avis : deux méthodes possibles.

La plus rigoureuse sans doute du point de vue mathématique : considérer T comme une fonction de l'unique variable g et effectuer un développement de Taylor limité au premier ordre :

$\triangle T=T(g_{0}+\triangle g)-T(g_{0})\approx\triangle g\cdot\left(\frac{\partial T}{\partial g}\right)_{g=g_{0}}$
La seconde méthode, un peu moins rigoureuse mais souvent tolérée en physique, a l'avantage de donner directement la variation relative de T : il s'agit de la méthode dite ” de différentiation logarithmique ”. Elle consiste à écrire l'expression du logarithme népérien puis à différentier en considérant g comme seule variable :

$\ln\left(T\right)=\ln\left(2\pi\right)+\frac{1}{2}\ln\left(\frac{mh^{2}}{3}+Mx^{2}\right)-\frac{1}{2}\ln\left[K-g\left(Mx+\frac{mh}{2}\right)\right]$

$\frac{dT}{T}=-\frac{1}{2}\cdot\frac{d\left[K-g\left(Mx+\frac{mh}{2}\right)\right]}{\left[K-g\left(Mx+\frac{mh}{2}\right)\right]}=\frac{\left(Mx+\frac{mh}{2}\right)\cdot dg}{2\left[K-g\left(Mx+\frac{mh}{2}\right)\right]}$
Les variations étant supposées faibles, sont assimilées aux différentielles :

$\frac{\triangle T}{T_{1}}\approx\frac{\left(Mx+\frac{mh}{2}\right)\cdot\triangle g}{2\left[K-g_{0}\left(Mx+\frac{mh}{2}\right)\right]}=\frac{\triangle g}{g_{0}}\cdot\frac{\left(Mx+\frac{mh}{2}\right)\cdot g_{0}}{2\left[K-g_{0}\left(Mx+\frac{mh}{2}\right)\right]}$

Posté par re : Mécanique 9 02-08-16 à 20:51

Mon intuition était donc la bonne.

Merci pour ça !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Mécanique 9

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique