Bonjour,

Cette fois-ci, il va plutôt s'agir d'une vérification, et d'une demande pour une autre méthode de résolution.
Voici tout d'abord l'énoncé :
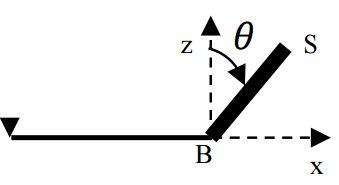
On considère un arbre, modélisé par une tige indéformable , de masse , de longueur . On le scie à la base et l'arbre bascule en tournant autour de son point d'appui au sol . On suppose que le point d'appui reste fixe et ne glisse pas. A , l'abre fait un angle avec la verticale et est immobile. On donne le moment d'inertie de l'arbre par rapport à l'axe . Déterminer le temps de chute d'un arbre de 30 mètres. On donne .

En utilisant la conservation de l'énergie mécanique, je trouve :

.

En arrangeant un petit peu, et en séparant les variables :

.
En intégrant de , je trouve :

.
Est-ce correct ?

Et une autre question me vient : Pourquoi nous donner le moment d'inertie ?