Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

Mécanique 5

Posté par
Flewer47 30-07-16 à 17:19

Bonjour,

Voici un exercice (encore un autre oui, sûrement pas le dernier) qui me donne du mal :

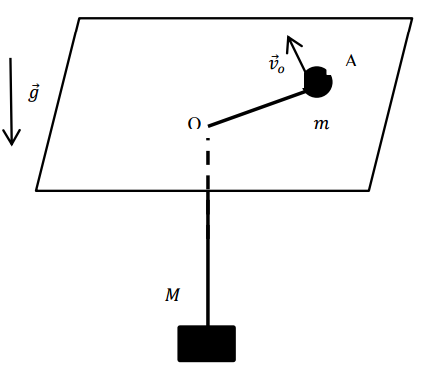
On considère un petit mobile en A, de masse m posé sur une table. La table est percée d'un trou en O, par lequel passe un fil de longueur L, relié au mobile, l'autre extrémité étant relié à une masse M. Initialement, le mobile a une vitesse \vec{v_0}, perpendiculaire au fil et la longueur du fil sur la table est r_0. (On suppose je pense l'absence de frottements sur la table et dans l'air, ainsi que la liaison parfaite)
Décrire le mouvement du mobile. Le mouvement peut-il être circulaire ? On note r=OA.

J'ai pensé d'abord à dire que le moment cinétique du mobile se conserve, et j'obtiens après ça (passage en coordonnées polaires) : 2\frac{dr}{dt}\frac{d\theta}{dt}+r\frac{d^2\theta}{dt^2}=0.
Ensuite, j'ai utilisé le fait que le système était conservatif pour dire que l'énergie mécanique se conservait.
J'obtiens alors \frac{d^2r}{dt^2}\frac{dr}{dt}+r\frac{dr}{dt}(\frac{d\theta}{dt})^2+r^2\frac{d\theta}{dt}(\frac{d\theta}{dt})^2=0.

Je ne vois pas trop comment continuer pour me débarrasser des vitesses angulaires..

Mécanique 5

Posté par
Flewer47re : Mécanique 5 30-07-16 à 17:25

Pardon pour ma confusion, il n'y a pas de liaison en O évidemment.

Posté par
vanoisere : Mécanique 5 30-07-16 à 17:34

OK pour la conservation du moment cinétique en O de la masse m.
Effectivement, si on néglige les frottements au niveau du trou ainsi que l'énergie nécessaire à la déformation du fil, il y a conservation de l'énergie mécanique mais il s'agit de l'énergie mécanique de l'ensemble {m,M}.
Tu as raison d'utiliser les coordonnées polaires ; le point A va décrire une spirale.

Posté par
vanoisere : Mécanique 5 30-07-16 à 18:09

Citation :
le point A va décrire une spirale

Dans le cas suggéré par le schéma où M semble très supérieure à m : oui. On peut cependant imaginer un cas particulier de vitesse initiale Vo où le mouvement de A est circulaire et uniforme. On peut aussi imaginer des vitesses Vo suffisamment importantes pour que r commence par augmenter au cours du temps.
Autre remarque : tout compte fait, il me semble plus simple d'appliquer la RFD à la masse m en coordonnées polaires et à projeter selon  Ur et U (tu retrouves au passage l'équation de conservation du moment cinétique déjà obtenue). Tu peux ensuite appliquer la RFD à M en considérant que la tension se conserve le long du fil considéré comme inextensible et de masse négligeable. L'équation différentielle vérifiée par r n'est pas simple dans le cas général... On te demande peut-être de la résoudre dans des cas particuliers...

Posté par
Flewer47re : Mécanique 5 30-07-16 à 21:45

En fait, on pourrait peut-être plutôt faire cela énergétiquement :
Par conservation du moment cinétique, on a \frac{d\theta}{dt}=\frac{r_0v_0}{r^2}.
Par conservation de l'énergie mécanique, on a :
\frac{1}{2}(m+M)\frac{dr}{dt}^2+\frac{1}{2}mr^2(\frac{d\theta}{dt})^2+Mgr=\frac{1}{2}mv_0^2+Mgr_0 (en prenant l'énergie potentielle nulle quand toute la corde est passée par le trou en 0, i.e. si on prend z=0 pour la table, alors Epp(\frac{-l-r}{2})=0).
Cette relation devient avec ce qui est dit plus haut :
\frac{1}{2}(m+M)\frac{dr}{dt}^2+\frac{1}{2}m\frac{r_0^2v_0^2}{r^2}+Mgr=\frac{1}{2}mv_0^2+Mgr_0

On a un peu une sorte d'énergie potentielle effective, le mouvement circulaire serait alors pour le r tel que cette énergie potentielle effective soit minimum, non ?

Posté par
Flewer47re : Mécanique 5 30-07-16 à 21:46

soit minimale* pardon.

Posté par
Flewer47re : Mécanique 5 30-07-16 à 21:47

Pour ce qui est de la trajectoire du mobile, je pense qu'il suffit juste de dire que pour un r_0 plus petit que celui pour le mouvement circulaire, le mobile spirale vers le trou, tandis que pour l'inverse, le mobile spirale vers l'extérieur jusqu'à faire remonter la masse M jusqu'à O, non ?

Posté par
vanoisere : Mécanique 5 30-07-16 à 23:31

Ton message du   30-07-16 à 21:45 me convient parfaitement. L'idée de l'énergie potentielle effective est excellente. J'avais de mon côté appliqué la RFD, ce qui m'a conduit à :

\left(M+m\right)\cdot\ddot{r}=\frac{m\cdot r_{0}^{2}\cdot V_{0}^{2}}{r^{3}}-M\cdot g
Si tu dérives par rapport au temps ton expression, tu arrives au même résultat.
Le minimum de Ep(eff) ou (au choix) la condition : r=r_{0}\;\forall t\;soit\;\ddot{r}=0\;\forall t conduit à l'expression de la vitesse initiale correspondant à un mouvement circulaire uniforme, la masse M restant immobile :

V_{0C}=\sqrt{\frac{M\cdot g\cdot r_{0}}{m}}
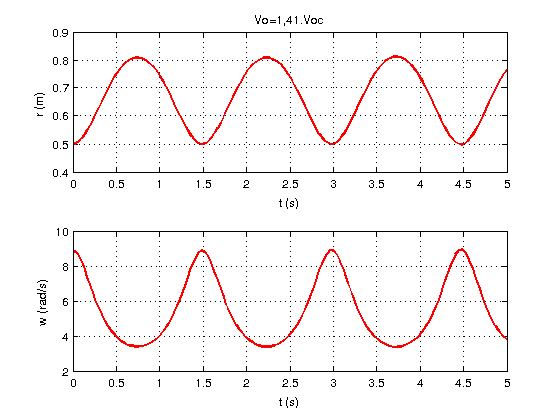
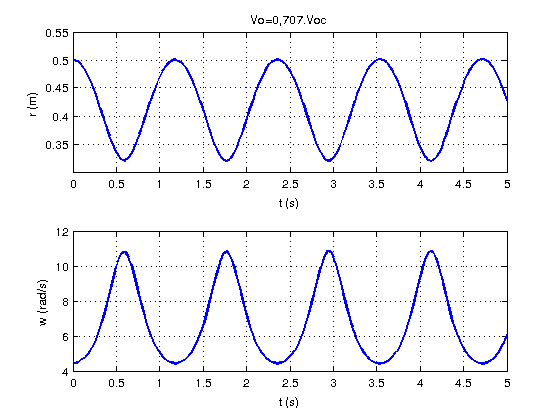
Sous réserve que le fil soit suffisamment long pour que ni m ni M ne viennent heurter la table, r varie périodiquement entre la valeur ro et une valeur rmax si Vo>Voc et r varie périodiquement entre ro et une valeur rmin si Vo<Voc.
Voici, pour illustrer cela, une simulation numérique sous MATLAB dans le cas Vo=Voc.2 (courbes rouges) et une autre simulation pour Vo=Voc/2 (courbes bleues).
Sont représentées simultanément les variations en fonction du temps de r et de la vitesse angulaire . J'ai choisi au hasard :
m=0,200kg ; M = 0,400kg ; ro=0,500m
En choisissant une valeur de Vo proche de Voc, un developpement limité devrait conduire à une variation de r de la forme :

r=r_{0}+A\cdot\left[1+\cos\left(\omega t+\varphi\right)\right]

Mécanique 5

Mécanique 5

Posté par
Flewer47re : Mécanique 5 31-07-16 à 00:11

Merci pour cette réponse claire et détaillée.
Cependant, je ne comprends pas comment tu arrives à la conclusion que le mouvement du mobile varie périodiquement entre 2 positions, ainsi que la relation donnée par ta RFD : je n'arrive pas à comprendre comment ton premier terme du membre de droite apparaît..

Posté par
vanoisere : Mécanique 5 31-07-16 à 00:34

\frac{d\left(\frac{1}{2}\dot{r}^{2}\right)}{dt}=\ddot{r}\cdot\dot{r}\quad;\quad\frac{d\left(\frac{1}{2r^{2}}\right)}{dt}=-\frac{\dot{r}}{r^{3}}
Il faudrait connaître la fin de l'énoncé pour être capable de dire laquelle des deux méthodes est la plus pertinente dans ce contexte.
Pour montrer que r oscille entre deux valeurs, le raisonnement sur l'énergie potentielle effective est très indiqué, sur le modèle de ce que tu as fait à propos du mouvement des satellites. Sinon, la RFD montre bien que le signe de \ddot{r} change régulièrement. Aucun des deux raisonnements ne permet de trouver la période. Pour cela il faut faire un développement limité si Vo est proche de Voc. Si cette approximation n'est pas possible, il faut à mon avis se contenter d'une résolution numérique comme j'ai fait...
Mais bon : mes remarques n'ont peut-être pas d'intérêt dans le contexte de ton énoncé. Poste-le et on en reparlera si tu veux.

Posté par
Flewer47re : Mécanique 5 31-07-16 à 01:01

J'ai compris pour la dérivation, ce n'est pas ça le problème, c'est le terme \frac{m\cdot r_{0}^{2}\cdot V_{0}^{2}}{r^{3}} qui apparaît dans ton PFD, je ne comprends pas à quelle force cela correspond.

Je poste toujours l'entièreté des énoncés des exercices sur lesquels je travaille, donc il n'y a rien après.

Posté par
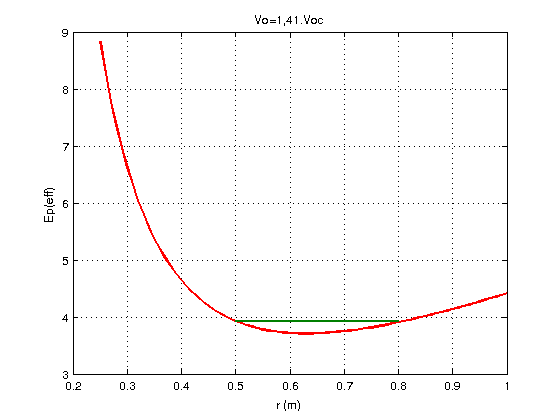
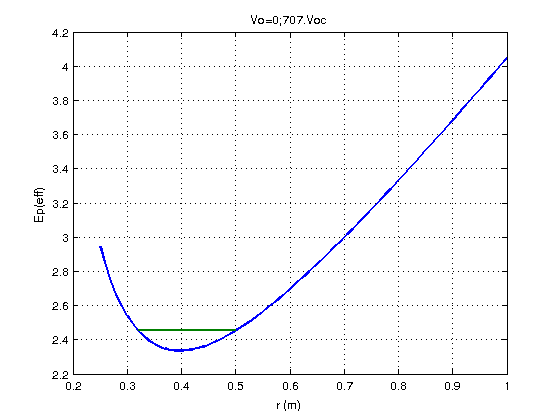
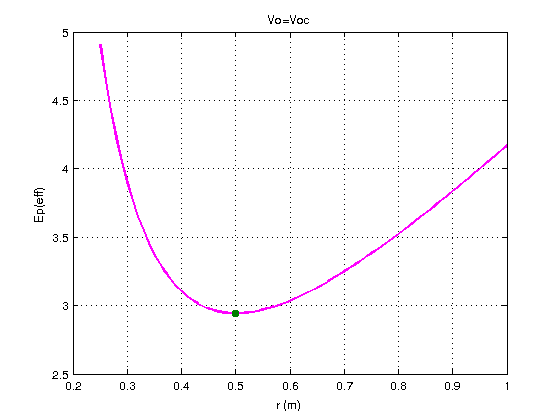
Flewer47re : Mécanique 5 31-07-16 à 01:03

Non, pardon, au temps pour moi, je l'ai.

Posté par
Flewer47re : Mécanique 5 31-07-16 à 01:04

Merci encore !
Et à très bientôt ! (Oui, je n'ai pas fini d'embêter..)

Posté par
vanoisere : Mécanique 5 31-07-16 à 12:41

Vu le peu de temps que cela prend sous MATLAB, voici, pour illustrer ta méthode concernant l'énergie potentielle effective les courbes représentant les variations en fonction de r de l'énergie mécanique (horizontale verte se réduisant à un point pour Vo=Voc) et de l'énergie potentielle effective dans les trois cas :
Vo=Voc.2 ; Vo=Voc/2 ;
Vo=Voc.
Evidemment :

Ep(eff)=\frac{1}{2}m\frac{r_{0}^{2}v_{o}^{2}}{r^{2}}+Mgr\quad;\quad Em=\frac{1}{2}mv_{0}^{2}+Mgr_{0}

Mécanique 5

Mécanique 5

Mécanique 5

Posté par
Flewer47re : Mécanique 5 31-07-16 à 14:50

Je vois.
Il faut étudier le signe de E_m-E_{p,eff} pour connaître le mouvement. Je pense que juste dire s'il est impossible, circulaire, borné, ou non borné suffit de répondre à la question.

Sinon, un développement limité autour de la position pourrait aider. Ce n'est pas demandé ici du moins.

Merci beaucoup pour ces illustrations !

Posté par
vanoisere : Mécanique 5 31-07-16 à 22:39

Citation :
Sinon, un développement limité autour de la position pourrait aider

Je crois qu'il y a déjà un moment que nous avons débordé du cadre strict de l'énoncé mais cela peut te préparer à d'autres problèmes analogues et à t'entraîner aux calculs. Comme déjà dit, l'équation différentielle n'admet pas de solution analytique simple à cause du r3 au dénominateur. Il faut se contenter de résolution numérique avec un logiciel spécialisé (MATLAB, SCILAB, Maple...). En revanche, un développement limité peut se faire si la vitesse initiale est proche de celle conduisant au mouvement circulaire. Voici le calcul à partir de l'équation différentielle du mouvement. L'étude peut aussi se faire en montrant que le ” fond ” de la cuvette correspondant à la courbe Ep(eff)=f(r) est assimilable à une branche de parabole dans ce cas particulier.

V_{0}=V_{oc}\left(1+\alpha\right)=\left(1+\alpha\right)\sqrt{\frac{M.g.r_{0}}{m}}\quad avec\quad|\alpha|\ll1
Je cherche une solution de la forme :

r=r_{0}+u=r_{0}\left(1+\frac{u}{r_{0}}\right)\quad avec\quad|u|\ll r_{0}
Sachant que, au premier ordre près :

\left(1+x\right)^{n}\approx1+n.x\quad si\quad|x|\ll1 et : \left(1+x\right)\left(1+y\right)\approx1+x+y\quad si\;|x|\ll1\;et\;|y|\ll1 :

m\frac{r_{0}^{2}V_{0}^{2}}{r^{3}}=m\frac{r_{0}^{2}\left(1+\alpha\right)^{2}.M.g.r_{0}}{mr_{0}^{3}\left(1+\frac{u}{r_{0}}\right)^{3}}=M.g.\left(1+\alpha\right)^{2}\left(1+\frac{u}{r_{0}}\right)^{-3}\approx M.g.\left(1+2\alpha-3\frac{u}{r_{0}}\right)
L'équation différentielle se simplifie en remarquant : \ddot{r}=\ddot{u} :

\left(m+M\right)\ddot{u}-2M.g.\alpha+3\frac{M.g}{r_{0}}\cdot u=0

Je te laisse finir si cela t'intéresse, tu vas obtenir une solution de la forme indiquée dans mon message du 30/7 à 23h31 avec une pulsation :

\omega=\sqrt{\frac{3M.g}{\left(m+M\right)\cdot r_{0}}}

Voici la simulation avec MATLAB pour \alpha=0,04.

Mécanique 5

Posté par
Flewer47re : Mécanique 5 31-07-16 à 23:01

Je vois comment vous avez fait. C'est instructif. Merci beaucoup pour ces bonus !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !