Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

Mécanique 4

Posté par
Flewer47 29-07-16 à 23:42

Bonsoir,

Voici un exercice qui me donne du mal :
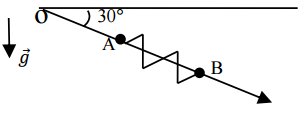
Deux points matériels A et B de masses respectives m_A=m et m_B=\frac{m}{3} (m=1kg) sont astreints à se déplacer sans frottements sur une droite formant un angle de 30°=\alpha avec l'horizontale. Ils sont reliés par un ressort de longueur à vide l_0 et de constante de raideur k.
1) Le point A étant fixé en 0, déterminer les positions d'équilibre de B et la période des petites oscillations autour de lui.
2) Le système étant à l'équilibre, on libère le point A. Déterminer x_A(t) et x_B(t).
3) Calculer l'énergie mécanique totale du système.

J'ai trouvé pour la 1) :
x_{B,éq}=\frac{mgsin(\alpha)}{3k}+l_0, et les petits mouvements autour de cette position d'équilibre sont sinusoïdaux de période T=2\pi \sqrt{\frac{m}{3k}}.

Je bloque cependant pour la 2).. Il me semblerait qu'on peut dire que l'énergie mécanique de A se conserve et celle de B aussi : on aurait alors 2 équations et on pourrait s'en sortir avec un couplage éventuel des variables.. Mais je ne sais pas comment exprimer l'énergie potentielle élastique de A et de B dans le cas où on lâche A...

Posté par
Flewer47re : Mécanique 4 29-07-16 à 23:43

Voici l'image :

Mécanique 4

Posté par
J-Pre : Mécanique 4 30-07-16 à 09:38

Proposition (je n'ai pas essayé de faire les calculs).

Energie potentielle élastique du ressort : Epe = 1/2.k.(xB - xA - Lo)²

Energie potentielle de pesanteur de l'ensemble : Epp = - mA.g.xA.sin(alpha) -  mB.g.xB.sin(alpha)  (avec niveau des Epp = 0 au point O)

EcinA = 1/2.mA.VA² (avec VA = dxA/dt)

EcinB = 1/2.mB.VB² (avec VB = dxB/dt)

E mécanique ensemble = Epe + Epp + EcinA + EcinB = Constante

En dérivant par rapport au temps --> une équation d'inconnues xA(t) et xB(t)

En remarquant que la force exercée par le ressort sur A et de même amplitude mais de sens contraire à celle exercée par le ressort sur B -->

mA.d²xA/dt² = - mB.d²xB/dt² (2eme équation d'inconnues xA(t) et xB(t))

Sauf distraction (ou erreur)  

Posté par
vanoisere : Mécanique 4 30-07-16 à 12:01

Bonjour

Citation :
je n'ai pas essayé de faire les calculs

Cela se voit car la relation de conservation de l'énergie, écrite d'ailleurs à mon avis correctement, ne conduit pas à une simple relation entre xA et xB mais à une relation entre les deux abscisses, les deux vitesses et les deux accélérations : rien de très simple et de facile à exploiter.
Citation :
Sauf distraction (ou erreur)

Je parlerais plutôt d'erreur :
Citation :
En remarquant que la force exercée par le ressort sur A et de même amplitude mais de sens contraire à celle exercée par le ressort sur B -->

mA.d²xA/dt² = - mB.d²xB/dt² (2eme équation d'inconnues xA(t) et xB(t))

Le système formé des deux masses n'est pas isolé : son centre d'inertie accélère sous l'action des forces de pesanteur !
Je préfère de loin l'intuition de Flewer47 qui parle de système couplé !
Si on applique la RFD à chaque masse et que l'on projette sur l'axe incliné, on obtient un système d'équations couplées :

\begin{cases} \\ m_{A}\ddot{\cdot x}_{A}=m_{A}\cdot g\cdot\sin\left(\alpha\right)+k\left(x_{B}-x_{A}\right)\\ \\ m_{B}\ddot{\cdot x}_{B}=m_{B}\cdot g\cdot\sin\left(\alpha\right)-k\left(x_{B}-x_{A}\right) \\ \end{cases}}
La somme membre à membre nous donne une première relation entre les accélérations. Elle nous donne accessoirement aussi l'accélération du centre de masse qui, contrairement à ce qu'a écrit JP, n'est pas nulle. Après division des termes de la première relation par mA et des termes de la seconde par mB, une soustraction membre à membre conduit à une seconde relation entre les deux accélérations faisant intervenir la masse réduite.

\ddot{x}_{A}-\ddot{x}_{B}+\frac{k}{\mu}\left(x_{A}-x_{B}\right)=0\quad\text{avec : \ensuremath{\frac{1}{\mu}=\frac{1}{m_{A}}+\frac{1}{m_{B}}}}

Ainsi (xA-xB) apparaît comme une fonction sinusoïdale du temps de pulsation \omega=\sqrt{\frac{k}{\mu}}. Ayant ainsi (xA-xB) et \left(m_{A}x_{A}+m_{B}x_{B)}\right) tu peux conclure. Le mouvement de chaque masse est la composition d'un mouvement uniformément accéléré et d'un mouvement oscillatoire sinusoïdal de pulsation \omega.

Posté par
Flewer47re : Mécanique 4 30-07-16 à 12:30

Bonjour J-P, merci d'avoir pris le temps de répondre.

Pour la deuxième équation, que fais tu du poids, qui en A n'est pas l'opposé de B ?

Posté par
Flewer47re : Mécanique 4 30-07-16 à 12:34

D'accord, merci Vanoise !
J'ai juste du mal à exprimer la force du ressort en A et en B. Pourquoi prend-elle cette forme là, et pourquoi la longueur à vide du ressort ne nous intéresse plus dans ce cas-là ? (Ou du moins, pourquoi cela n'apparaît plus ?)

Posté par
vanoisere : Mécanique 4 30-07-16 à 13:25

Tu as raison : j'ai oublié lo dans les formules. Merci pour la remarque ! Cela ne change pas la méthode heureusement : la dérivée seconde de \left(x_{A}-x_{B}-l_{0}\right) est égale à la dérivée seconde de \left(x_{A}-x_{B}\right)
\begin{cases} \\ m_{A}\ddot{\cdot x}_{A}=m_{A}\cdot g\cdot\sin\left(\alpha\right)+k\left(x_{B}-x_{A}-l_{0}\right)\\ \\ m_{B}\ddot{\cdot x}_{B}=m_{B}\cdot g\cdot\sin\left(\alpha\right)-k\left(x_{B}-x_{A}-l_{0}\right) \\ \end{cases}

\ddot{x}_{A}-\ddot{x}_{B}+\frac{k}{\mu}\left(x_{A}-x_{B}-l_{0}\right)=0\quad\text{avec : \ensuremath{\frac{1}{\mu}=\frac{1}{m_{A}}+\frac{1}{m_{B}}}}
Pour être sûr de ne pas te tromper de signe dans les projections des forces exercées par le ressort sur les deux masses : suppose (xB-xA)>lo. Le ressort est plus long qu'à l'équilibre ; il tend à revenir à sa longueur à vide en exerçant sur A une force orientée dans le sens + et en exerçant sur B une force orientée dans le sens négatif.

Posté par
vanoisere : Mécanique 4 30-07-16 à 13:34

Une précision concernant les actions exercées par le ressort : si tu appliques la RFD au ressort en supposant sa masse d'influence négligeable, tu montres simplement que la force exercée par la masse A sur le ressort et la force exercée par la masse B sur le ressort sont deux forces de vecteurs opposés. En appliquant le principe des actions réciproques (principe de l'action et de la réaction), tu en déduis que les forces exercées par le ressort sur la masse A et sur la masse B sont deux forces de vecteurs opposés.

Posté par
Flewer47re : Mécanique 4 30-07-16 à 14:12

Effectivement, merci pour ça !
Tu as oublié de changer le signe devant l_0 lorsque tu l'as ramené à gauche. Je bosse sur ça et je reviens !

Posté par
vanoisere : Mécanique 4 30-07-16 à 14:57

Dans ces conditions, il est préférable  de soustraire (1) de (2) après division par les masses respectives comme déjà expliqué :

\ddot{x}_{B}-\ddot{x}_{A}=-\frac{k}{\mu}\left(x_{B}-x_{A}-l_{0}\right)

En posant : X=\left(x_{B}-x_{A}-l_{0}\right) allongement du ressort, tu obtiens l'équa. dif. :

\ddot{X}+\frac{k}{\mu}\cdot X=0
Ensuite, ayant l'expression en fonction de t de X et de \left(m_{A}x_{A}+m_{B}x_{B}\right), tu peux conclure.

Posté par
Flewer47re : Mécanique 4 30-07-16 à 15:06

On a donc :
m_A\frac{d^2x_A}{dt^2}+m_B\frac{d^2x_B}{dt^2}=(m_A+m_B)gsin(\alpha) \text{  }(1) \\ \frac{d^2x_A}{dt^2}-\frac{d^2x_B}{dt^2}+\frac{k}{\mu}(l_0+x_A-x_B)=0 \text{  } (2)
On a \mu = \frac{m}{4} \text{ et } m_A+m_B=\frac{4}{3}m.

De (2) on tire :
(x_A-x_B)(t)=-\frac{mgsin(\alpha)}{3k}cos(2\sqrt{\frac{k}{m}}t)-l_0 \text{  } (3)   car (x_A-x_B)(0)=-x_{B,eq} \text{ et } (\frac{dx_A}{dt}-\frac{dx_B}{dt})(0)=0.
D'où :
\frac{d^2x_A}{dt^2}=\frac{4gsin(\alpha)}{3}cos(2\sqrt{\frac{k}{m}}t)+\frac{d^2x_B}{dt^2}

En réinjectant dans (1) :
x_B(t)=\frac{gsin(\alpha)}{2}t^2+\frac{mgsin(\alpha)}{4k}cos(2\sqrt{\frac{k}{m}}t)+\frac{mgsin(\alpha)}{12k}+l_0  car x_B(0)=x_{B,eq} \text{ et } \frac{dx_B}{dt}(0)=0.
Et enfin, en réinjectant dans (3) :
x_A(t)=\frac{gsin(\alpha)}{2}t^2-\frac{mgsin(\alpha)}{12k}cos(2\sqrt{\frac{k}{m}}t)+\frac{mgsin(\alpha)}{12k}.

Posté par
Flewer47re : Mécanique 4 30-07-16 à 15:08

Désolé Vanoise, je t'ai devancé sur ce coup-là, j'écrivais ma réponse pendant que la tienne est apparue !

Pour la troisième question, je pense utiliser la conservation de l'énergie mécanique totale du système, puisque celui-ci est conservatif.

Posté par
J-Pre : Mécanique 4 30-07-16 à 15:23

Citation :
"Je parlerais plutôt d'erreur"


Pourquoi pas, puisque cela te fait tant plaisir.

Posté par
Flewer47re : Mécanique 4 30-07-16 à 15:46

Pas besoin d'utiliser la conservation, il suffit d'écrire et de remplacer et on a tout.
Merci beaucoup pour votre aide !

Posté par
vanoisere : Mécanique 4 30-07-16 à 15:50

Super , Flewer47 ! Le plus dur du point de vue physique est fait. Les cosinus au carré qui vont intervenir dans l'expression de Ep devraient se simplifier avec les sinus au carré qui vont intervenir dans l'expression de Ec pour donner une expression indépendante du temps... Bon courage pour les calculs !

Posté par
vanoisere : Mécanique 4 30-07-16 à 15:52

Bravo ! Mon dernier message était inutile compte tenu de ton niveau !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !