Inscription / Connexion Nouveau Sujet
mecanique
bonjour,
c'est encore moi !! 
j'ai un exercice de mecanique cette fois, par contre je n'ai aucune idée de la facon dont je dois m'y prendre pour le resoudre.
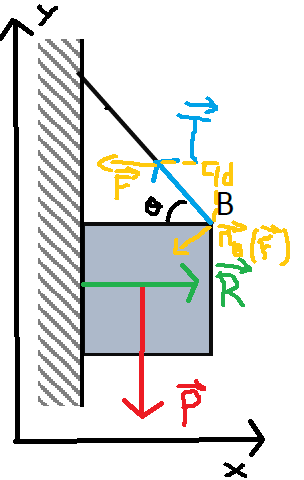
Est-ce qu'il est possible d'attacher un cube au mur vertical (voir la figure) en absence du
frottement ?
donc j'ai fait le bilan des forces
P= poid du cube
R= reaction du support
T= tension du fil
 = angle entre le mur et le fil
= angle entre le mur et le fil
Je vais faire les projections et vous les transmettre des que j'aurais reussis lol
Par contre je ne vois absolument pas comment resoudre se probleme.
De prime abord pour moi ce n'est pas possible, si le cube est juste tenu par le fil, le cube ne peut pas se coller contre le mur.
comment prouver que le cube ne reste pas coller a la paroie (ou le contraire), peut etre faut il prouver que les force ne s'equilibre pas? que  F
F 0
0
A part ca je ne vois pas, auriez vous un debut de piste le temps que je fasse les projections?
Merci beaucoup
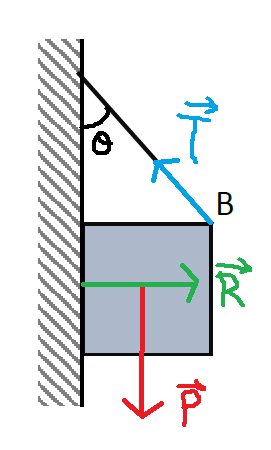
Bonjour
L'équilibre est possible si la résultante des forces extérieures est le vecteur nul et si la somme des moments des forces en tout point est le vecteur nul.
La projection des forces ne pose pas de problème. Je te laisse réfléchir ; tu vas constater qu'il est tout à fait possible d'avoir une résultante des forces nulles, les intensité T et R s'exprimant simplement en fonction de P et de  .
.
En revanche, ton intuition est exacte : l'équilibre correspondant à ta figure est impossible à obtenir en absence de frottement car il est impossible d'obtenir un moment nul des forces. Il ne faut pas supposer à priori que l'action du mur se réduit à une force de vecteur R appliquée au milieu de la face du cube en contact avec le mur. On peut démontrer, mais cela est un peu plus subtil, que l'équilibre en absence de frottement n'est possible que si le câble est fixée à une distance du mur inférieure à la demie longueur de l'arête du cube.
Je ne sais pas si la notion de moment de force t'est familière. Si non : laisse tomber cet exercice à titre provisoire.
PS : pas sûr que le concepteur de cet exercice ait autant d'intuition que toi et ait vu la difficulté posée... 
Re bonjour et encore merci pour ton aide.
Effectivement je n'avais pas penser au moments des forces.
J4ai commence du coup avec les forces sur le schema (aque j'ai un peu modifier, changer l'angle etc...) et fait mes projections (en esperant qu'elle soit correcte)
vect P : Px =0 vect T: Tx= -Tcos vect R: Rx=R
vect R: Rx=R
Py = -P Ty= Tsin  Ry=0
Ry=0
P+T+R=0
Px + Tx + Rx =0 0 - Tcos + R =0
+ R =0
Py + Ty + Ry =0 -P + Tsin + 0= 0
+ 0= 0
je me retrouve avec R= Tcos  et P= - Tsin
et P= - Tsin
la je bute
pour le moment de force, je l'ai indiquer sur le schema en jaune, je n'ai qu'un seul moment au point B? ce qui me fait
Mb(F) = T  F
F
donc le module vaut ||Mb(F)||=F.T.sin =F.d
=F.d
et ca doit etre egale a 0?
desolé je n'ai pas vu ton post avant de poster le mien.
On a le cours sur le moments des forces. meme si je galere un peu, je dois savoir le faire pour les exam de janvier.
De plus cette exercice et le dernier d'un devoir que je doit rendre demain donc je ne peut pas l'abandonner, meme si le devoir n'est noté que sur 5 et que ca ne changera pas ma moyenne, j'aimerais comprendre et avancer.
Attention : d'une figure à l'autre, tu as remplacé  par son complémentaire !
par son complémentaire !
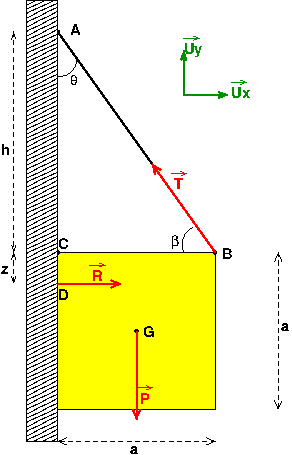
Ensuite, tu peux t'intéresser à la somme des moments au point A : point de fixation du câble dans le mur en notant "a" la longueur de l'arête du cube.
Je te poste un schéma légendé après le déjeuner.
ok ca marche je vais aller manger aussi.
Pour teta c'est normal j'ai preferé prendre cette angle pour mes projection, c'est plus simple du coup l'angle en face fait 90-teta
bonne appetit
Si l'angle  est défini par l'énoncé, il faut respecter cette notation. Pense à un correcteur un jour d'examen ou de concours avec une centaine d'étudiants (ou plus...) modifiant à leur gré les notations ! En revanche, si cela peut t'aider, rien ne t'empêche de raisonner d'abord sur l'angle en B mais il faut lui donner un autre nom.
est défini par l'énoncé, il faut respecter cette notation. Pense à un correcteur un jour d'examen ou de concours avec une centaine d'étudiants (ou plus...) modifiant à leur gré les notations ! En revanche, si cela peut t'aider, rien ne t'empêche de raisonner d'abord sur l'angle en B mais il faut lui donner un autre nom.
Traditionnellement, pour un vecteur quelconque, la lettre V désigne la norme de ce vecteur, valeur positive ou nulle alors que les notations Vx, Vy désigne les composantes algébriques de ce vecteur. En clair, tu as ici :
mais :
Tu vas arriver logiquement sans difficulté à exprimer T et R en fonction de P et  .
.
Pour aller plus loin et montrer que l'équilibre est en fait impossible en absence de frottement, tu peux essayer de voir s'il est possible d'obtenir une somme des trois moments nuls en A (voir figure).
La pression exercer par le mur sur le solide n'est pas nécessairement unforme sur toute la face du cube en contact avec le mur. Je suppose donc la réaction appliquée en D à la distance z de C, z n'étant pas a priori égal à (a/2). L'équilibre n'est possible que si la condition d'équilibre conduit à une valeur de z comprise entre zéro et a.
Le plan de figure est le plan vertical contenant le centre de gravité G du cube supposé homogène.
bonjour,
merci pour ta reponse.
Desolé pour le delai, c'est un peu la course, avec les greves ont ne sait pas si on pourra passer nos examen mardi (tp obligatoire) et si on ne vient pas normalement c'est zero. Bref galere galere
Pour theta, c'est moi qui l'a choisis, l'ennoncé ne precise rien juste:
" Est-ce qu'il est possible d'attacher un cube au mur vertical (voir la figure) en absence du frottement ?"
avec le schema sur lequel j'ai dessiné, la seul lettre qui apparrait sur le schema c'est B.
Pour T j'obtient t= -P/sin et R = (-P/sin
et R = (-P/sin ) cos
) cos  = -P/tan
= -P/tan
Par contre pour les moments pourquoi au point A et pas au point B?
Ok pour la notation de l'angle. En revanche : j'insiste : pour éviter les confusions de signes lors des projections , je pense que tu as intérêt à tenir compte de mon message précédent. P désigne la norme du vecteur poids, Px et Py pouvant être éventuellement négatifs.
Ton énoncé est donc tout à fait correct. Il te suffit de montrer que, si la résultante des forces peut être le vecteur nul, il est impossible d'avoir simultanément un moment résultant nul en tout point. J'ai choisi de m'intéresser au moment en A car le moment en A de la tension est nul, les deux autres moments étant simples à exprimer. Faire le raisonnement en G conduirait à un moment du poids nul mais à un moment de la tension moins simple à exprimer.
c'est ce que j'ai fait, sur mon 2eme schema j'ai bien mis mes axes dans le meme sens que les tient, du coup j'ai Px qui vaut zero forcement et Py qui est negatif.
Par contre meme en ayant trouver T et R, je ne vois pas comment prouver que la resultante des forces est nulle.
"si la résultante des forces peut être le vecteur nul, il est impossible d'avoir simultanément un moment résultant nul en tout point"
la je ne comprend pas, si les resultantes des forces est nul, le systeme est a l'equilibre, donc la resultantes des moments devrait etre nul aussi?
Pour qu'un équilibre soit possible, il faut simultanément une résultante des forces nulle et un moment résultant nul.
Pour démontrer l'absence d'équilibre, il faut donc démontrer que les deux conditions précédentes ne peuvent pas être vérifiées simultanément. Pour démontrer que cette simultanéité est impossible, on peut commencer par postuler une résultante des forces nulle puis démontrer que cette hypothèse est incompatible avec une somme des moments nulle.
bonjour,
merci pour ta reponse. Je comprend mieux, mais je n'ai plus le temps il faut que je rende ce devoir ce soir, par contre je laisse tomber pour aujourd'hui mais je reviendrais dessus pour essayer de le terminer
Je te copie l'essentiel sans détailler les calculs. Je reprends les notations de mon schéma précédent.
On fait l'hypothèse d'une résultante nulle des forces extérieures. Par projection cela conduit directement à :
Je vais démontrer que ces égalités sont incompatibles avec une somme des moments nulle. Faisons l'hypothèse d'une somme des moments nulle au point A pour démontrer que cela est incompatible avec l'hypothèse d'une résultante des forces nulle.
Je saute les intermédiaires de calcul ; cela conduit à :
Or :
En reportant au-dessus :
Cette valeur est totalement aberrante ! La pression exercée par le mur sur le cube n'est pas uniforme sur toute la face du cube en contact avec le mur. Nous n'avons donc pas nécessairement z=(a/2) mais, z est nécessairement compris entre zéro et a.
Conclusion : il est impossible d'avoir simultanément une résultante nulle des forces et une somme de moments nul. L'équilibre sans frottement est donc impossible.
A titre d'approfondissement, je te laisse démontrer qu'un équilibre serait possible pour un point de fixation B situé à une distance du mur inférieure à (a/2).
bon allez j'ai quand meme envie de le faire.
Je n'etait absolument pas la pour les moment mais tout s'eclaire maintenant. Je suis en train de refaire les calcul. Deja tu avait raison pour P j'ai oublier un - quelques part, (erreur d'inattention encore)corrigé.
pour vecAB j'ai ABx=a et ABy= -h donc AB T j'obtient bien 0
T j'obtient bien 0
Pour vecAG AGx= a/2 et AGy= -(h+a/2) (je pense que c'est ici que j'ai buggué)
donc AG P= -aP/2 + h + a/2
P= -aP/2 + h + a/2
vec AD ADx=0 et ADy = (h+z) donc AD R = R(h+z)
R = R(h+z)
du coup ma resultante j'ai h+a/2 en trop par rapport a toi
Mais AG sur y j'ai bien (-h+a/2) non?