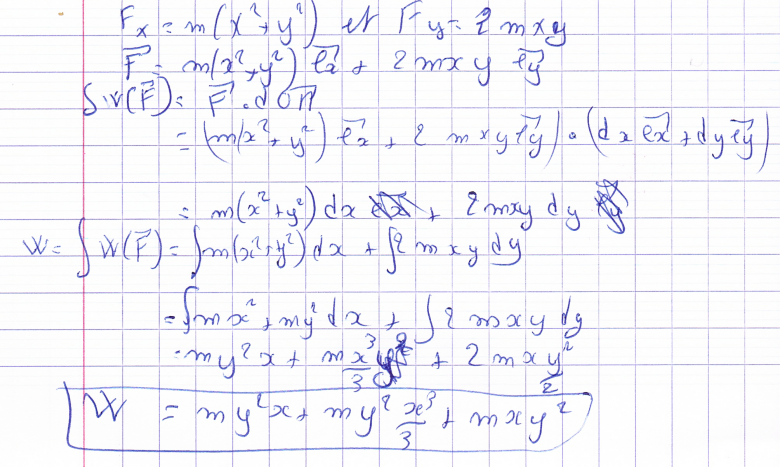Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

mecanique

Posté par
seif987552 30-01-18 à 18:08

bonsoir
Dans le plan fixe horizontal P(O,ex,ey) on donne un champ de force defini par les remations : Fx=m(x2+y2) et Fy=2mxy
Montrer que F derive d'une fonction potentielle que l'on determinera

Posté par
seif987552re : mecanique 30-01-18 à 18:09

veuillez m'aider
j'ai essaie de monter que le travaille est indépendant du chemain suivi m'ai j'ai pas reussi

Posté par
seif987552re : mecanique 30-01-18 à 18:19

voila ce que j'ai fait

mecanique

Posté par
vanoisere : mecanique 30-01-18 à 18:21

Bonjour
Connais-tu la notion de gradient ? Si oui, il suffit de vérifier :

\overrightarrow{F}=-\overrightarrow{grad}\left(E_{p}\right)

Posté par
seif987552re : mecanique 30-01-18 à 18:24

comment le faire svp

Posté par
vanoisere : mecanique 30-01-18 à 18:29

Je crois que nos derniers messages se sont croisés...
Réponds à la question sur le gradient car il s'agit de la méthode la plus simple. Si la réponse est non, je t'indiquerais une méthode alternative.

Posté par
seif987552re : mecanique 30-01-18 à 18:31

je ne sais pas comment manipulier le grad

Posté par
seif987552re : mecanique 30-01-18 à 18:32

manipuler

seif987552 @ 30-01-2018 à 18:31

je ne sais pas comment manipulier le grad

Posté par
vanoisere : mecanique 30-01-18 à 18:55

OK : il est possible de s'en passer mais il faut quand même avoir quelques notions mathématiques sur les différentielles. Je pars de ton expression du travail élémentaire qui est correcte :

\delta W=m\left(x^{2}+y^{2}\right)dx+2mxy.dy

Si la force dérive d'une énergie potentielle, ce travail est l'opposé de la variation élémentaire d'énergie potentielle :

dE_{p}=-\delta W=-m\left(x^{2}+y^{2}\right)dx-2mxy.dy

Ep est une fonction de x et y et dEp est une différentielle :

dE_{p}=\left(\frac{\partial E_{p}}{\partial x}\right)dx+\left(\frac{\partial E_{p}}{\partial y}\right)dy

par identification :

\left(\frac{\partial E_{p}}{\partial x}\right)=-m\left(x^{2}+y^{2}\right)\quad;\quad\left(\frac{\partial E_{p}}{\partial y}\right)=-2mxy

Pour répondre à la question 1, il suffit de montrer que dEp est bien une différentielle : elle doit vérifier le théorème de Schwarz :

\left(\frac{\partial^{2}E_{p}}{\partial x\partial y}\right)=\left(\frac{\partial^{2}E_{p}}{\partial y\partial x}\right)

Le théorème est bien vérifié :

\left(\frac{\partial\left(-m\left(x^{2}+y^{2}\right)\right)}{\partial y}\right)=\left(\frac{\partial\left(-2mxy\right)}{\partial x}\right)=-2my

La force dérive bien d'une énergie potentielle. Il suffit alors de trouver Ep telle que :

\begin{cases} \\ \left(\frac{\partial E_{p}}{\partial x}\right)=-m\left(x^{2}+y^{2}\right)\\ \\ \left(\frac{\partial E_{p}}{\partial y}\right)=-2mxy \\ \end{cases}

Je te laisse terminer...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !