Niveau maths sup

Mécanique

Posté par
kinaricu 06-01-18 à 12:07

Bonjour,

J'aimerai avoir votre avis sur mes réponses à la question suivante :

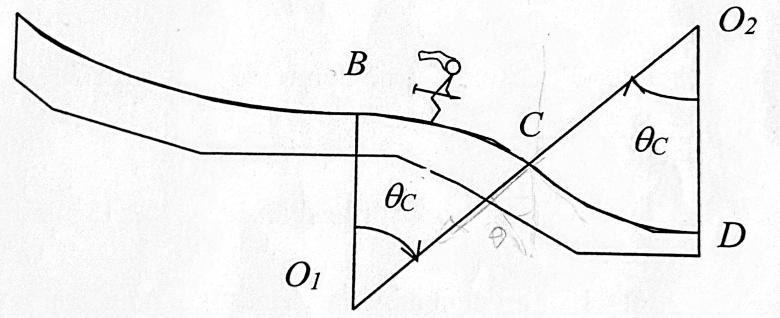
Un skieur aborde des bosses avec une vitesse $V_0 = 10 m/s$ en B. (schéma en bas du message)
On néglige tout frottement.
Le profil de la piste est représenté par deux arcs de cercle de rayon $R_c$ et d'angle $\theta_c = 20 °$ . On néglige la taille du skieur devant $R_c$

a) Ecrire les lois du mouvement du skieur dans le repère de coordonnées polaires.
b) Exprimer la valeur de la réaction de la piste sur le skieur en fonction de l'angle $\theta$ .
A quelle condition sur $R_c$ le skieur reste-t-il au contact de la piste en C.
c) Pour la valeur précédente limite de $R_c$ calculez l'accélération ressentie par le skieur en D.

Mes réponses :

a) En appliquant le PFD sur un repère polaire et en projetant :

Selon $\vec{U_r} : -mR_c\dot{\theta}^2 = -cos(\theta)mg + R_N$
Selon $\vec{U_\theta} : mR_c\ddot{\theta} = sin(\theta)mg$

b) D'après la première équation ci-dessus :
$R_N = cos(\theta)mg-mR_c\dot{\theta}^2$
et donc $R_N = cos(\theta)mg-m\frac{v^2}{R_C}$

La condition de contact est $R_N > 0$
$\Leftrightarrow m(-gcos(\theta) - \frac{v^2}{R_C} >0$
$\Leftrightarrow R_C > \frac{v^2}{gcos(\theta)}$

c) (Je suis moins sur de moi pour celle-ci)

Avec le PFD sur le deuxième arc de cercle :

Selon $\vec{U_r} : -mR_c\dot{\theta}^2 = cos(\theta)mg + R_N$
Selon $\vec{U_\theta} : mR_c\ddot{\theta} = sin(\theta)mg$

et donc $\ddot{\theta} = \frac{sin(\theta)g}{R_c}$
et en D $\theta = 0$
donc l'accélération est nulle en D.

Voilà merci à la personne qui m'aidera !
Bonne journée

Mécanique

Posté par re : Mécanique 06-01-18 à 14:03

Bonjour
Je réponds d'abord à la première question.
L'application de la RFD est correcte. Pour étudier la condition de contact en C, il faut exprimer la vitesse du skieur en C. Cela peut se faire à l'aide du théorème de l'énergie cinétique appliqué entre les positions B et C.
Je te laisse rectifier toi-même !

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Mécanique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique