Bonjour Touker,

Tu peux étudier le mouvement (circulaire uniforme ) de l'une des boules depuis un référentiel terrestre.
La boule étudiée est soumise à deux forces non négligeables :
- Son poids
- La tension de la tige
La deuxième loi de Newton te permettra de trouver ce que tu cherches.

Bien sûr, tu peux aussi étudier le mouvement de la boule à partir d'un référentiel lié à cette boule. Ce référentiel n'étant pas galiléen, il faudra penser à introduire une force d'inertie centrifuge comme terme correctif.
A toi de choisir en fonction de ton niveau et de tes préférences la méthode la plus adaptée.

Alors voila ce que j'ai fait :
Seconde loi de Newton appliquée à une des boules, j'écris l'expression du vecteur accélération puisque la vitesse angulaire w est constante.
Du coup je projette le vecteur unitaire e_r sur (Oz) (que j'ai mis ascendant) et j'ai
Est-ce correct ?

Bonsoir,

J'ai des doutes sur ce que tu as écrit, mais il est possible que tu utilises des notations qui m'échappent.
Je me contente de projeter sur la base cylindrique la relation
et je trouve comme demandé une relation entre ,,g et L

Peux tu détailler la projection (en particulier le sin(a)) ?

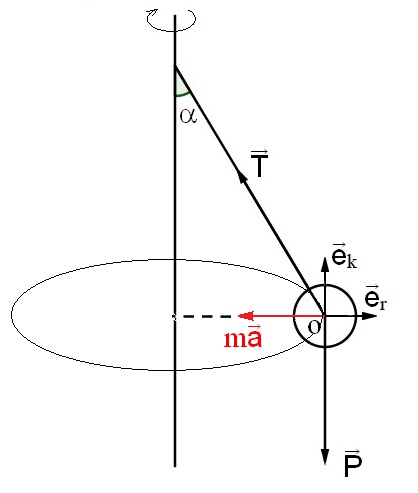
Ci joint un schéma qui, je pense, éclaircit mon calcul.
Pour simplifier, je n'ai représenté que deux vecteurs unitaires , car les composantes de toutes les forces suivant le 3e axe sont nulles.

D'acc je n'avais pas orienté, mes vecteurs comme ça

Euuuh... je projette sur quel axe pue égaliser ? Il y a un truc qui cloche, que z je n'ai pas ce que je veux

Bonjour,

Projection sur l'axe de vecteur unitaire :
0 - T.sin() = -m.L.²sin()
soit après simplification :
T = m.L.²

Projection sur l'axe de vecteur unitaire :
-m.g + T.cos() = 0

En combinant ces deux relations on répond à la question posée.