Bonsoir
Tu y est presque !
En écrivant qu'au cours des oscillations, la longueur du ressort est (Le+x) puis en simplifiant l'équation différentielle ainsi obtenue en tenant compte de la condition d'équilibre, tu devrais arriver simplement à :


Pour la résolution, tout dépend de la valeur de : les solutions sont différentes selon que est inférieur, égal ou supérieur à .
Pour la 4) : as-tu étudié l'utilisation des complexes en régime sinusoïdal ?

Bonsoir,

Je vous remercie beaucoup.
Je ne vois pas comment arriver au résultat que vous avancer car je traîne la fonction g, j'ai g- * x.
Quant à la résolution, tout dépend de , d'accord est-ce que c'est la même chose que dire que 0 ?
Pour moi les complexes en régime sinusoïdal était tout ce qui traitait de l'impédance, non ?

Bonjour
Au cours du mouvement, à un instant quelconque de date t, la longueur du ressort est : L = Le+x . L'énoncé est clair là-dessus : x représente le déplacement par rapport à la position d'équilibre. La force exercée par le ressort sur la masse m a pour expression :



Soit en tenant compte de la condition d'équilibre que tu as obtenue :



La relation fondamentale de la dynamique, appliquée dans le repère terrestre supposé galiléen conduit à :



Cela conduit bien à l'équation que je t'ai fournie hier soir. Pour la résolution de cette équation différentielle, tu vas constater qu'étudier le signe de revient à comparer à ...

Pour l'étude du régime sinusoïdal forcé, tu as deux méthodes possibles : l'utilisation des complexes comme en électricité, l'utilisation des vecteurs de Fresnel. Si tu est habitué à utiliser les complexes en électricité, je pense que tu as intérêt à choisir cette méthode...

Bonjour,

Je vous remercie de vos explications. Je m'y remets de ce pas et continue la résolution.

Bonsoir,
Est-ce ceci ?

4) la réponse de l'oscillateur est :
x(t)= x''+2x'+ =
x(t)=xg(equation homogène) + xp(solution particulière
xg= plusieurs cas selon , mais peut-on dire que xp = ?

5) si on part de Q= , la bande passante demandé est le ?

Pour la 4) : quand on soumet l'oscillateur à l'excitation périodique de pulsation , on obtient d'abord un régime transitoire de courte durée non étudié ici suivi d'un régime où x est fonction sinusoïdale du temps de même pulsation que l'excitation. Ce régime est qualifié de " régime sinusoïdal forcé" car la pulsation des oscillations est celle imposée par l'excitation.
Bref : tu dois te limiter ici à l'étude d'une solution de la forme :


où Xm est l'amplitude des oscillations et le déphasage entre x(t) et F(t).
L'équation différentielle est bien celle que tu as écrite :


Comme en électricité, à chaque grandeur sinusoïdale, tu peux associer une grandeur complexe dont le module est l'amplitude et dont l'argument est la phase. Cela te conduit à poser :


x est alors solution de l'équation :


Il te faut alors exprimer Xm et en fonction des différentes données...
Je te laisse réfléchir à tout cela et proposer une solution. N'hésite pas à poser des questions complémentaires si nécessaire.
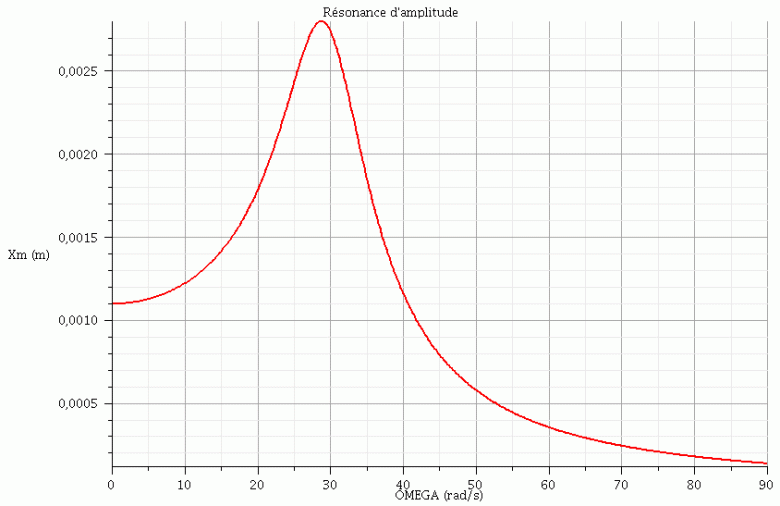
Pour la question 5, il s'agit sans doute d'étudier les variations de Xm en fonction de la pulsation d'excitation . Tu vas obtenir un phénomène de résonance d'amplitude : la courbe Xm=f() va présenter un maximum pour une valeur de un peu inférieure à la pulsation propre de l'oscillateur.
Sans que cela ne présente dans ce contexte un grand intérêt, l'énoncé demande de poser :


où Q est le facteur de qualité de l'oscillateur.

Mauvaise position des parenthèses dans deux formules que je recopie ci-dessous après rectification :

Quelques précisions :
Je n'avais pas vérifiée encore l'expression de la condition d'équilibre et pas du tout pris en compte le fait que les oscillations s'effectuent le long d'un plan incliné d'un angle par rapport à l'horizontale... Cela conduit à remplacer g par g.sin() dans tous les calculs. Heureusement, cela modifie l'expression de la longueur (Le) du ressort à l'équilibre mais ne modifie pas les équations différentielles vérifiées en mouvement d'oscillations libres puis en mouvement d'oscillations forcées.

Je t'ai parlé de la résonance d'amplitude. Voici la courbe Xm=f() dont je t'ai parlé (en rouge). J'ai posé Q=2,5 comme dans l'énoncé mais j'ai choisi pour la pulsation propre une valeur arbitraire : =30rad/s.
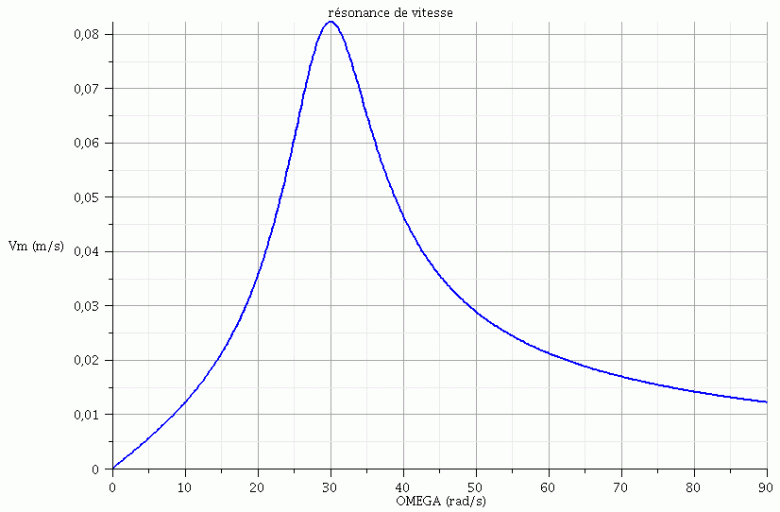
Il existe une autre résonance intéressante : la résonance de vitesse : on s'intéresse aux variations en fonction de de l'amplitude de la vitesse : Vm=.Xm (courbe bleue). Ton énoncé parle de réponse de l'oscillateur sans plus de précision. Il s'agit probablement de l'étude de la résonance d'amplitude mais si tu pouvais obtenir plus de renseignements...

Je vous remercie beaucoup.

Pour illustrer la notion de régime d'oscillations forcées, voici la courbe x=f(t) correspondant à la solution complète de l'équation différentielle déjà évoquée :


J'ai choisi comme précédemment une pulsation propre =30rad/s, et un facteur de qualité Q=2,5. J'ai choisi une pulsation d'excitation =20rad/s et j'ai supposé à l'instant initial la vitesse nulle et x = 0. La courbe bleu correspond à la sinusoïde d'équation et la courbe rouge correspond à x = f(t). Tu va remarquer qu'après un court régime transitoire (environ trois période d'excitation), la courbe x = f(t) est assimilable à une sinusoïde de même période que celle de la force d'excitation mais les deux sinusoïdes présente un déphasage. on peut alors poser : ; le régime sinusoïdal forcé est obtenu après une durée très courte : ici environ trois périodes de la force d'excitation.
Remarque : échelle verticale arbitraire.