Utilise la conservation de l'énergie mécanique.



Exprime en fonction de et , en fonction de .

oui mais je pense qu'il faut le faire avec la deuxième loi de newton ce qui donnerai en projetant
On a P+R=ma

sur ox mg-Rcos=m a_x
sur oy 0 +Rsin=m a_y

mais après je vois pas trop

Tu penses? C'est-à-dire qu'on t'impose une méthode?

Dans ce cas, il vaut mieux projeter sur les vecteurs radiaux et orthoradiaux

Et projeter l'accélération sur les même vecteurs:



En appliquant la deuxième Loi de Newton, on obtient:




On a besoin uniquement de la deuxième équation que l'on multiplie de chaque côté par puis on intègre pour trouver la relation demandée.

s'il vous plait, personne ne peut m'aider?

donc en multipliant on obtient
mr d²/d²t *d/dt =-mgcos*d/dt

on intègre on obtient

mr d/dt=-mgsin?

Pas tout à fait:



Et n'oublie pas que l'égalité que l'on trouve après intégration n'est exacte qu'à une constante près qu'il te faut ajouter et déterminer.

je peux vous poser une question pourquoi dans la deuxième projection on obtient
mr d²/d²t c'est pas plutot mrd/dt  car a=dv/dt

j'ai rien dis j'ai dis une betise

par contre quand je fais les projections je trouve cela:

sur Ox mgcos-R=-mr(d/dt)²
sur Oy -mgsin=mrd²/dt²

Attention, on ne projette pas sur les axes que tu indiques.

Le résultat est de toute façon faux. Par exemple, la norme de la composante radiale du poids est maximale pour . Ta projection implique qu'elle est nulle pour cet angle!

Il faut toujours vérifier que le résultat est bien cohérent en prenant quelques points particuliers.

c'était sur er et e que j'avais fait la projection faute de frappe

je fais un schéma et pourtant je vois pas pourquoi vous avez une sin dans la projection sur er et où est passé le signe négatif pour l'accélération?

peut etre que l'on a pas le meme schéma l'axe Ox est verticale et Oy horizontale et est l'angle orienté (Ox,OM)

Effectivement, il y a une différence importante puisque ton angle correspond à l'angle avec la verticale.

Voici mon schéma:

Oui ce n'est pas le meme en effet....est ce que j'ai bon avec mon schéma?

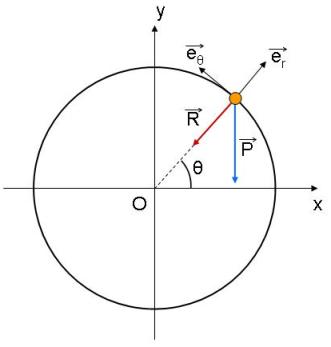
En ce qui concerne les sinus et cosinus, oui.

Pour les signes, ça dépend de l'orientation que tu donnes à tes vecteurs. A priori, la projection sur est incorrecte.

merci beaucoup pour votre aide j'ai vu mon erreur
Bonne journée