Inscription / Connexion Nouveau Sujet
Mécanique
Bonjour,
J'aurais besoin d'aide pour cet exercice :
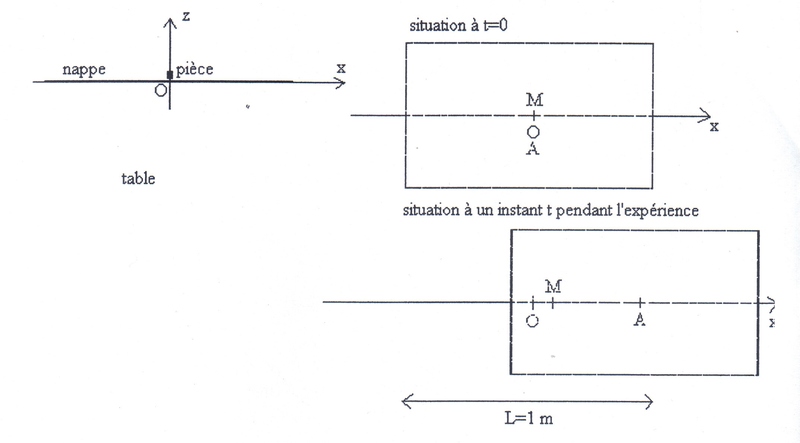
Le voici, sur la table rectangulaire de longueur L=1m, recouverte d'une nappe sans ourlet, de même dimension, on dépose une pièce. D'un geste brusque, on tire la nappe. La pièce reste en place sur la table. La nappe, repérée par son centre A, a une masse M=200g. La pièce M est assimilable a une masse ponctuelle m=10g. La force développée par l'expérimentateur pendant qu'il tire sur la nappe est F=M
t.
ouest le vecteur unitaire directeur de l'axe Ox et une constante. Le frottement entre la nappe et la table est négligeable, celui entre la nappe et la pièce est caractérisé par le coefficient de frottement dynamique f1=0.75. On note g l'accélération de la pesanteur. Le référentiel est supposé galiléen.
1) On admet que la pièce commence à glisser sur la nappe dès le début de l'expérience. Préciser le sens de la vitesse de glissement definie comme la différence entre la vitesse de la pièce et celle de la nappe. en déduire les caractéristiques de la réaction tangentielle de la nappe sur la pièce
-Alors pour cette question, j'ai répondu que le sens de la vitesse est dans le sens de l'axe Ox. La pièce n'étant pas immobile nous avons ||Rt||=f||Rn|| ou ||Rn|| = mg
2) On suppose dans un premier temps le contact entre la nappe et la pièce En appliquant le PFD à M, déterminer l'équation differentielle satisfaite par l'abscisse xm de M et la resoudre
-Ici j'ai beaucoup plus de mal et je n'arrive pas à un resultat.
J'écris : ||Rt|| + Mt = m . a ou a = d²xm/dt²
j'ai alors fmg + Mt = ma
Mais je ne vois pas comment je peux obtenir une équation differentielle de cela :s
Merci de toute aide que vous pourriez m'apporter 
Les forces exterieures sont a determiner
Il ya le poids la reaction du plan la force de frottement et la force developpée par l'experimentateur
C'est une action de contact elle agit par frottement
Sinon j'ai verifié il manque rien il y a un 3) et 4) apres c'est tout
Que signifie alors :
2) On suppose dans un premier temps le contact entre la nappe et la pièce
?
Si la pièce a commencé à glisser, il n'y a plus de raison pour qu'elle subisse l'influence de la force exercée sur la nappe.
Ouii c'est vrai mais alors notre equation differentielle
S'écrit fmg = ma
et on a toujours pas d'equation diffrentielle en fonction de xm enfin on a juste a=d²x/dt²
On me dit ensuite faire un bilan soigneux des forces sur la nappe. Comment en particulier peut on determiner la reaction de la piece sur la nappe à l'aide de la question 2? En deduire l'equation différentielle satisfaite par l'abscisse xa du centre A de la nappe. La resoudre pour obtenir l'équation horaire de xa(t)
Alors bilan des forces sur la nappe:
Poids, reaction du plan, la force de frottement de la nappe sur la table (négligeable), force exercée par l'expérimentateur.
P + Rn + F = m.a
Mais comment determiner la reaction de la piece sur la nappe?
Oui Rnappe->piece = - R pièce -> nappe
Or Rnappe->piece= f1 * m * g
on a aussi P = -Rn
Alors l'équation differentielle donne :
M*t - f1*m*g = ma or a = d²xa/dt²
Et on integre comme on a fait plus haut:
xa = M/m * 1/6 * t^3 - 0.5 * f1 * g * t²
est ce que cela est juste?
Pour moi ce t^3 me parait bizarre :s Ce ne serait pas un probleme d'integration mais je n'ai pas l'habitude de voir ce type d'équation horaire en physique :s
)
Mais cette solution n'est elle pas "bizarre?"
Surtout lorsque nous lisons la dernière question
"En negligeant le deplacement de la piece devant celui de la nappe, determiner l'instant t0 ou la piece quitte la nappe. Calculer xm(t0) et vm(t0). Quelle doit etre la valeur de pour que xm(t0)= 5 cm? Quelle est alors l'intensité maximale de la force developpée par l'opérateur pendant l'experience."
Comment ça? Pourtant tu es bien en mesure d'exprimer la position du centre de la nappe en fonction du temps, non?
C'est une donnée. On ne peut pas à la fois caractériser le mouvement et déterminer la valeur des forces extérieures qui lui donnent naissance. Il faut que l'on nous donne quelques informations tout de même...
je sais bien, c'est pour cela que je me demande si ce n'est pas l'équation differentielle qui est fausse ... Puisque dans l'énoncé nous n'avons aucune information sur
Si le mouvement était indépendant de , cela impliquerait qu'il est indépendant de l'intensité de la force qu'on applique à la nappe, non?
Dans ce cas, je ne réponds plus de rien...
Au contraire, puisque l'on te demande justement de déterminer la valeur de pour une configuration donnée.
La piece quitte la nappe lorsque xa a parcouru 0.5 m
xa = * 1/6 * t^3 - 0.5 * f1 * m/M *g * t² cette expression nous permet pas de determiner notre t0 puisque nous sommes bloqué avec . Ou je dois raté un truc énorme :s 
Je saute cette partie determiner t0 puisque je bloque toujours,
Je reponds donc à ces questions "Quelle doit etre la valeur de pour que xm(t0)= 5 cm? Quelle est alors l'intensité maximale de la force developpée par l'opérateur pendant l'experience."
5.10^-2 / (0.5 * f1 * g) = t²
En remplacant par les valeurs de l'énoncé on a :
t0 = 0.116 s
La valeur de est donc
= (x
= ( xa + 0.5f1 * m / M * g * t0²)/ (1/6 * t0^3) = 1906.8
Soit l'intensité maximale de la force developpée par l'opérateur durant l'experience :
F = M * t0 = 44 N
Oui Rnappe->piece = - R pièce -> nappe
Or Rnappe->piece= f1 * m * g
on a aussi P = -Rn
Alors l'équation differentielle donne :
*M*t - f1*m*g = Ma or a = d²xa/dt²
Il me semble avoir fait une erreur ici en effet on a Rnappe->piece= m * g
P + Rn = 0 cela ne change pas
on a donc
*M*t + m*g = Ma
Quelqu'un pourrait me confirmer??
Merci d'avance
Annuler
connectez vous