Inscription / Connexion Nouveau Sujet
meca solide rotation : calcul de moment d'inertie
Bonjour à tous
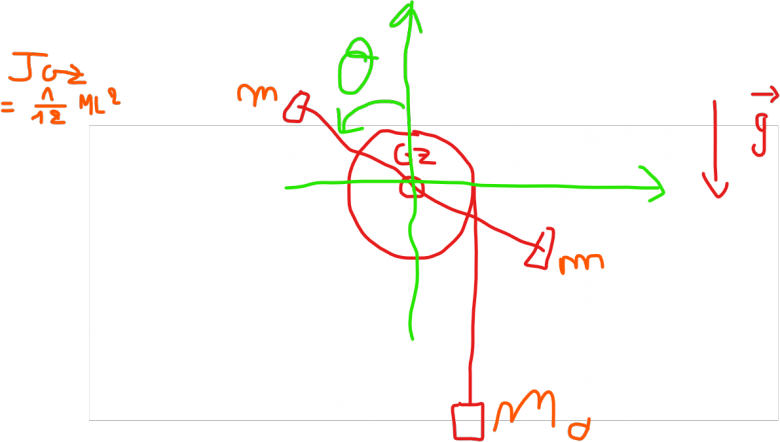
on considère la figure suivante (cf image).
On note : L la longueur de la tige, M sa masse. m la masse de chacune des deux petites masses accrochées aux extremites de la tige. R le rayon du disque. r la distance d'une masse à G. On nous donne la valeur de J_GZ comme vous pouvez le voir sur le schéma.
J'essais de chercher l'équation du mouvement.
j'ai trouvé que le moment cinetique de tout le systeme (tige, masses m, masse m0 et disque) vaut : Lz=(Jgz+2mr²+m0R²)w.
on peut appliquer le TMC.
Le moment du poids des petites masses sannule et il reste finalement le moment du poids de m0 : -m0gR par bras de levier.
Donc :
(Jgz+2mr²+m0R²)dw/dt=-m0gR
Mais cette équation me paraît étrange. En effet quand on intègre on a w à constance près (cette constante est nulle car par hypothese w(0)=0). donc a donc w qui est une fonction lineaire. Ceci est étrange, car ça ne devrait pas du tout être le cas...
J'ai par ailleurs une autre question : comment peut-on déterminer le moment d'inertie de la tige autour de l'axe avec un protocole expérimental. Je ne vois pas comment faire cette mesure.
Pouvez-vous m'aider ?
Je vous remercie par avance.
Seul le moment d'inertie par rapport à l'axe de rotation de la partie tournante est à prendre en compte : ceux des deux masses ponctuelles, celui de la tige et celui du disque homogène mais la masse de ce disque ne semble pas indiquée...??? En tous cas, mo n'intervient pas dans l'expression du moment d'inertie.
bonjour vanoise,
merci pour votre réponse
j'ai du mal à vous comprendre. Pour quelle raison ne faudrait il pas prendre en compte le moment d'inertie de la masse m0 ? Il est à prendre en compte, comme tous les autres moments du solide, normalement.
Notons P le point situé à l'endroit de la masse m0.
Alors : (OP^m0v).u_z=m0*R²*w <- moment de m0.
Par rapport au repère terrestre supposé galiléen, le solide de masse mo est en mouvement de translation verticale. Il suffit donc de lui appliquer la relation fondamentale de la dynamique (ou théorème du centre d'inertie). En revanche, l'ensemble {disque, tiges, masses ponctuelles} constitue un solide mobile autour d'un axe fixe horizontal. Il faut lui appliquer le théorème du moment cinétique (ou moment dynamique). Il suffit ensuite de considérer que la tension garde la même norme le long du fil pour résoudre le problème.
Tu ne m'as pas répondu à propos des caractéristiques du disque...
Effectivement j'ai oublié de répondre pour les caractéristiques du disque. Le disque est de rayon R, on ne connaît pas sa masse.
Par ailleurs, j'ai oublié de dire que dans l'énoncé, il est dit que la distance entre une petite masse et G, notée r, est variable. J'ai du mal à comprendre le sens de cette hypothèse. Cela signifie que les masses ne sont pas fixées ? Je ne comprends pas... Je crois que les masses sont fixées, mais on peut les fixer à un autre endroit.
Je ne comprends toujours pas pourquoi vous ne voulez pas considérer le moment de m0. En effet on sait bien que dans un solide, il faut sommer les moments.
Concernant le disque. Son moment est négligeable face aux autres moments, c'est ce que l'énoncé nous pousse à remarquer.
Je me demande si tu ne confonds pas moment d'inertie d'un solide en rotation autour d'un axe et moment d'une force par rapport à un axe... Reprends attentivement mon message du 04-03-22 à 17:14.
Commence par établir l'expression de l'accélération "a" du solide de masse mo. Cette expression dépend de r. Je suppose qu'en TP, tu peux obtenir un tableau de mesures de l'accélération "a" pour différentes valeurs de r. Tu verras alors comment en déduire la valeur de :
PS : je ne connais pas ton matériel de TP ; peut-être que le moment d'inertie du disque est négligeable devant celui de la tige...
Aussi, concernant le protocole pour mesurer le moment d'inertie de la tige experimentalement ? Je vous remercie
Bonjour.
Je ne confonds pas moment d'un point et moment d'une force.
Le moment d'un point M est défini par OM^mv. Êtes vous d'accord pour dire que OP^mv_P où P est le point de la masse m0 vaut m0R²w ? C'est un calcul direct. Le système considérer est le système {disque, tiges, masses ponctuelles,masse m0} et non {disque, tiges, masses ponctuelles}
Bonjour, en fait je ne comprends pas non plus pourquoi vous dites que l'accélération de m0 dépend de r. Vous vous êtes trompé je pense. Celle-ci dépend de R (grand R), car elle vaut Rdw/dt.
Vous vous êtes trompé je pense.
Bien entendu, personne n'est à l'abri d'une erreur ou d'une étourderie (surtout pas moi) mais tout de même : je te trouve bien rapide à trouver que les gens qui n'obtiennent pas tes résultats se trompent !

L'accélération dépend effectivement de R mais elle dépend aussi du moment d'inertie du solide en rotation constitué de l'ensemble {deux masses, tige, disque}. Or ce moment d'inertie par rapport à l'axe de rotation dépend aussi de r...
Si tu veux vraiment comprendre l'intérêt du dispositif, il faut que tu commences par établir l'expression de l'accélération du solide de masse mo. Je t'ai fourni quelques indications à ce sujet dans mon message du 04-03-22 à 17:14.
Je n'aurais pas dû dire que vous vous êtes trompé. Visiblement, ça vous a perturbé.
On applique le PFD en m0 : m0.R.dw/dt = m0.g - T où T est la tension du fil. Je ne comprends pas à quoi ça nous sert, on se rajoute une inconnue : T.
L'inconnue "T" va disparaître si on applique le théorème du moment dynamique (ou théorème du moment cinétique) au solide mobile autour de l'axe (Gz). En effet : le fil étant de masse négligeable, la tension du fil a même norme tout le long du fil.
Je ne comprends pas ce que je dois faire. À quoi cela sert de calculer l'accélération du point m0 alors que cela nous est inutile pour le tmc ? J'ai du mal à vous suivre. J'ai l'impression que vous voulez appliquer le tmc au système privé de m0. Alors que moi j'applique le tmc au système entier.
Quelle expression de l'accélération du solide mo obtiens-tu ? Essaie d'expliquer la méthode que tu utilises.
J'essaie d'appliquer votre méthode, mais je ne sais pas ce que vous voulez que je fasse. Vous dites qu'il convient, dans cette situation, de faire un TMC. C'est ce que j'ai fait dès le départ. Vous m'avez dit que mon TMC n'était pas bon car selon vous le moment du pt m0 n'est pas à prendre en compte. (Je n'ai toujours pas compris pourquoi, d'ailleurs). Je crois comprendre que vous voulez que j'applique différemment le TMC.
Je ne vois pas comment appliquer le tmc grâce à ceci : m0.R.dw/dt = m0.g - T. Le tmc s'applique en calculant le moment d'inertie du solide, donc en déterminant le moment d'inertie de chaque point qui le compose, y compris le point m0. Dès lors, je ne comprends pas ce que je dois faire avec m0.R.dw/dt = m0.g - T. Concernant l'accélération de m0, j'imagine qu'il faut la déterminer grâce à votre méthode. Je ne parviens pas à l'appliquer, donc je ne sais pas. Je vous remercie.
D'accord. Je l'applique.
Notons Jz,tot le moment d'inertie du systeme total (comprenant notamment la masse m0). Jz,tot = (Jgz+2mr²+m0R²)w
Le terme en m0 est issu d'un calcul direct.
Ainsi : (Jgz+2mr²+m0R²)dw/dt=-m0gR (TMC)
où -m0gR est le moment du poids de m0 (immédiat par bras de levier)
C'est ce que j'ai fait dès le départ. Comment utiliser m0.R.dw/dt = m0.g - T ?
Normalement, en appliquant un TMC sur un tel système, on ne doit pas avoir de tension de fils, car les tensions de fils sont des forces internes au système.
Tu n'as absolument pas compris ce que j'essaie de t'expliquer depuis le début. Le système doit être considéré comme deux sous-systèmes :
1° : le solide en rotation de moment d'inertie par rapport à son axe de rotation(2mr2+J[sub]Gz[/sub) soumis non pas au poids mais à la tension du fils qui produit un moment par rapport à l'axe de rotation positif : T.R
2° : le solide en translation soumis à son poids et à la tension du fil à son extrémité inférieure, tension égale à l'opposé de la tension exercée par l'extrémité supérieure du fil sur le solide en rotation.
En combinant les deux relations, T disparaît et on obtient l'expression de l'accélération attendue.
Bonjour.
Effectivement je ne comprends rien de ce que vous me dites.
Essayons de nouveau. On applique le tmc sur le système {masses m, disque, tige} : (2mr²+J_GZ)dw/dt=T.R (le moment du poids des deux petites masses s'annule).
T=(1/R).(2mr²+J_GZ)dw/dt
pfd en m0 : m0.g-T=m0.a
en sommant ces deux identités : m0.g=(1/R).(2mr²+J_GZ)dw/dt+m0.a
Que faire de ceci ?
Je tiens à préciser que l'équation différentielle recherchée doit être en w.
En plus : le fil enroulé sur le disque ne glisse pas pas rapport au disque. La vitesse du fil, donc aussi la vitesse du solide en translation verticale, est égale à la vitesse d'un point à la périphérie du disque :
En dérivant par rapport au temps, tu obtiens une relation très simple entre l'accélération “a” du solide en translation et l'accélération angulaire du solide en rotation :
Oui, je suis d'accord. D'où :
(2mr²+J_GZ+m0R²)dw/dt=m0.g.R
Mais on retrouve exactement la relation que j'ai écrite dans mon tout premier message sur ce topic (à signe près, il doit y avoir une erreur de signe ou bien dans la nouvelle relation, ou bien dans la toute première)... Relation avec laquelle vous n'étiez pas d'accord.
C'est assez étrange de trouver que dw/dt>0 et donc w>0. En effet, on voit bien sur le schéma (étant donné l'orientation de theta), que la vitesse doit être négative, puisque le disque semble intuitivement tourner vers la droite.
J'ai évidemment choisi comme sens positif de rotation le sens correspondant au sens spontané du mouvement : celui de la descente du solide de masse mo. Si j'ai bien compris : il s'agit de mesurer l'accélération "a" de mo lors de son mouvement vertical vers le bas pour différents réglages de la distance "r" et d'en déduire la valeur de JGz.
En physique, tu as toujours intérêt à choisir les orientations correspondant à un minimum de signes négatifs. Il ne te viendrait pas à l'idée d'étudier une chute libre par rapport à un axe orienté vers le haut...
J'avais placé theta ainsi afin qu'il soit dans le sens de la base directe, mais peu importe. Aussi : j'ai du mal à comprendre pourquoi vous avez dit que mon équation initiale était fausse, alors que celle-ci est strictement la même que la vôtre.
Pouvez-vous détailler un peu plus le protocole pour mesurer le moment d'inertie de la tige svp ? Je ne vois pas vraiment en quoi mesurer l'accélération a pour différentes valeurs de r permet de le faire ?
L'accélération “a” vérifie :
A partir d'un tableau de mesures, tu places dans un repère les points de coordonnées (r2, 1/a). Si les mesures ont été faites avec soin, tu vas obtenir un ensemble de points sensiblement alignés le long d'une droite moyenne dont l'intersection avec l'axe vertical aura comme ordonnée :
D'où la valeur de JGz...
Dans mon premier message, le mot "faux" était effectivement abusif. Tout de même, quand tu dois étudier un ensemble de plusieurs solides reliés par des fils, des ressorts,...., tu as tout intérêt à étudier séparément le mouvement de chaque solide puis à tenir compte des liaisons même si, dans les cas simples comme ici, une méthode globale est possible. D'ailleurs, une autre méthode globale possible aurait consisté à raisonner sur la conservation de l'énergie mécanique puisque les frottements sont négligés.